Элементы зонной теории твердого тела, страница 6

Как видно из рисунка 3.4 дисперсия электронов в кристалле – довольно сложная функция. Однако, большинство явлений в кристаллах определяется электронами, заселяющими долины (обычно самую нижнюю по энергии из них). В долине, дисперсия электрона, как правило, параболическая: e= (элементы i и j пробегают значения x,y, и z). Если сравнить это выражение с выражением для энергии свободного электрона, то можно для данной квадратичной формы определить элементы тензора эффективной массы: 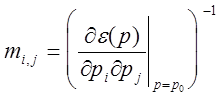. Вектор p₀- положение центра долины. Энергия электрона при этом запишется как e=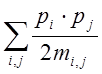 (обратите внимание, что это чётная функция от импульса). Обычно, можно выбрать главные оси, в которых тензор эффективной массы будет иметь диагональный вид. При этом компоненты тензора могут сильно отличаться для различных направлений, то есть, эффективная масса электронов в кристалле может быть анизотропной. Вдоль некоторых направлений электронам двигаться «легче», а вдоль других «тяжелее». Тензор эффективной массы определяет всю динамику электронов в долинах.

В кристалле существует множество электронов с некоторой разрешённой энергией вблизи дна долины. Вектор квазиимпульса этих электронов опишет некую фигуру, которая называется изоэнергетической поверхностью. В случае изотропной эффективной массы это сфера, для анизотропной эффективной массы это либо эллипсоид вращения, либо более сложные фигуры, сечение которых приведено на рисунке 3.5. По своей симметрии, эти фигуры должны соответствовать симметрии кристалла в точке центра долины. Так, в точке G в кристалле с ГЦК решёткой это кубическая симметрия. Легко заметить, что фигуры на рисунке 3.5 имеют ось вращения 4-ого порядка.

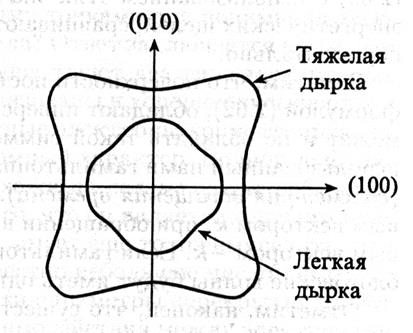
Рис. 3.5. Сечение плоскостью (001) изоэнергетических поверхностей для дырок в GaAs. Формулы, определяющая вид изоэнергетической поверхности приведены в книгах 2.1 и 2.3.

Мы уже пользуемся понятием «дырка», а сейчас попробуем разъяснить его смысл. При электромагнитном взаимодействии, сила, действующая на электрон пропорциональна его заряду, а импульс пропорционален эффективной массе. Так, второй закон Ньютона для электрона в кристалле, помещенном во внешнее электрическое поле с напряжённостью E, можно записать как: 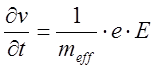. В кинетические коэффициенты (при электромагнитном воздействии) везде будет входить отношение заряда к эффективной массе. Как видно из рисунка 3.4, для валентных электронов, при увеличении квазиимпульса энергия уменьшается, значит их эффективная масса отрицательна. Как правило, валентная зона практически полностью заполнена электронами. Вклад в электрический ток от практически всех валентных электронов равен нулю, ведь практически каждому электрону с импульсом  найдётся его «антипод» с импульсом , а ток от них в сумме равен нулю. Зачастую бывает удобно описывать не движение электронов в почти полностью заполненной валентной зоне, а ввести понятие «дырки» - пустого места в валентной зоне. Такая квазичастица, при воздействии на неё электромагнитного поля будет вести себя как частица с положительным зарядом, но положительной массой. Фактически, при воздействии электромагнитного поля, движутся электроны, но их движение эквивалентно движению дырки. То есть при изучении вопросов касающихся переноса заряда (и энергии) в кристалле понятие дырки корректно, и упрощает кинетические уравнения. В дальнейшем, когда мы будем говорить об электронах, это как правило будет означать электроны зоны проводимости, о валентной зоне будем говорить как о зоне дырок. Но, не следует забывать, что и дырка и электрон – квазичастицы, скажем для гравитационного взаимодействия понятие эффективной массы и дырки не корректно. Более подробно с этим вопросом можно ознакомиться в §2 главы IV книги 2.3.

Лекция 6. Зонная структура основных полупроводников. Некоторые экспериментальные методы её исследования.

Прямозонные и непрямозонные полупроводники. Зонная структура основных полупроводников (Si, Ge, GaAs). Оптические и электрофизические методы исследования зонной структуры.

Если потолок валентной зоны и дно зоны проводимости находится в одной и той же точке зоны Бриллюэна, то такой полупроводник называют прямозонным полупроводником. Полупроводники, в которых потолок валентной зоны и дно зоны проводимости находится в разных точках зоны Бриллюэна, называются непрямозонными. Такое деление связано с особенностью оптических переходов в данных материалах, которые будут обсуждаться в разделе, посвящённом оптическим явлениям в полупроводниках.