Элементы зонной теории твердого тела, страница 5

В модели почти свободных электронов периодический потенциал кристалла рассматривается как возмущение. Наиболее радикальное влияние периодического потенциала это свёртка импульса электрона в пределы первой зоны Бриллюэна. И если в одномерном случае получится относительно простая дисперсия (примерно как на рисунке 3.3), то в случае трехмерного кристалла, даже простая свёртка параболической дисперсии (e=) даёт сложную картину, в которой возникают несколько энергетических зон [2.1]. К этому классу расчётных методов тяготеет метод псевдопотенциала и (k-p) метод.

В модели сильной связи (tight-binding) даже электроны внешних оболочек слабо взаимодействуют с соседними атомами, так как их волновые функции сильно локализованы на ионных остовах. Тем не менее, экспоненциальные «хвосты» волновых функций «дотягиваются» до соседних атомов и чувствуют их потенциал. Величина взаимодействия характеризуется интегралом перекрытия волновых функций соседних электронов [2.1, 2.6, 2.12], чем сильнее локализованы электроны, тем меньше интеграл перекрытия. Так как электроны взаимодействуют слабо, то их волновые функции почти такие же, что и в отдельных атомах. Поэтому, Блоховские функции можно построить из комбинации атомных волновых функций, взятых с множителем . Этот подход известен как метод линейной комбинации атомных орбиталей. Вследствие сильной локализации электронных волновых функций, атомные энергетические уровни слабо расщепляются в зоны, поэтому разрешённая зона для такого материала будет узкой, а (в случае большого расстояния по энергии уровней в атоме) запрещённая зона - широкой. Тем не менее данный метод может быть вполне применим и для расчётов узкозонных полупроводников.

На рисунке 3.4 показаны рассчитанные зависимости дисперсии энергетических уровней электронов в GaAs для двух кристаллографических направлений.

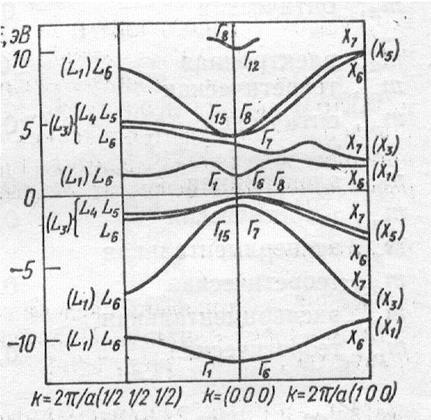
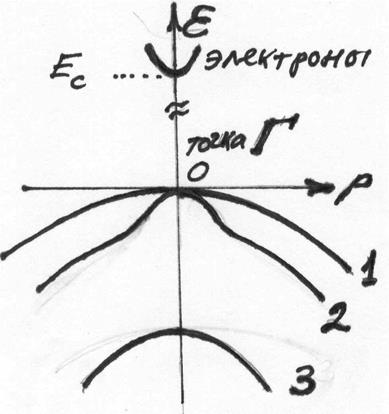
Рис. 3.4. Зонная структура GaAs (расчёт с учётом спин-орбитального расщепления, данные из справочника 3.7). Справа – увеличенная область центра зоны Бриллюэна: 1) зона тяжёлых дырок; 2) зона легких дырок; 3) отщеплённая за счет спин-орбитального взаимодействия зона.

Символы G₁₅, G₂ X₆ и т.д. – это общепринятые [2.1, 3.7] обозначения (предложенные Буккаэртом, Смолуховским и Вигнером – БСВ обозначения – Bouckaert L.P., Smoluchowski R.Wigner E., Phys. Rev. v.50, p.58, 1936), определяются они симметрией волновых функций в точках в соответствующих точках зоны Бриллюэна (G, X, и т.д.). За нулевой уровень энергии принят потолок валентной зоны. Три зоны валентных электронов (три кривые чуть ниже нуля) имеют два максимума в точке G (верхний двукратно вырожден) и минимумы на краях зоны Бриллюэна. Точки минимумов и максимумов на дисперсионных кривых называются долинами, и обозначаются, в соответствии с обозначениями точек в зоне Бриллюэна - G-, X-, либо L- долина. Так как в кристалле существуют эквивалентные направления, то существует и несколько эквивалентных долин (если они расположенные не в центре зоны Бриллюэна). Для кристаллов с кубической симметрией легко убедиться (сделайте это самостоятельно!), что если долина расположена вдоль направления, идущего из точки G в точку X (но не на границе зоны Бриллюэна), то таких долин 6 штук. Если долина расположена вдоль направления, идущего из точки G в L (но не на границе зоны Бриллюэна), то таких долин 8 штук. Необходимо отметить, что если центр долины попадает на край зоны Бриллюэна, то количество эквивалентных долин с центром в точке X , будет 3, а с центром в точке L – 4. Эквивалентность долин может быть нарушена внешним воздействием, приводящим к понижению симметрии кристалла, скажем, при приложении одноосного растяжения или сжатия. Для электронов в зоне проводимости (кривая чуть выше нуля) существуют свои долины, их положение не обязательно совпадает с положением долин в валентной зоне.