Элементы зонной теории твердого тела, страница 3

Так как в кубическом сантиметре кристалла находятся порядка 10²²-10²³ атомов, каждый содержит до нескольких десятков электронов, решить такое уравнение (найти собственные значения и волновые функции) невозможно.

Упрощение 1. Так как электроны, находящиеся на глубоких уровнях, слабо взаимодействуют с окружением атома, можно считать, что их волновые функции такие, как и в изолированном атоме. То есть мы разбили электроны на валентные электроны и электроны ионного остова. Вычисления волновых функций последних отдельная квантово-механическая задача атомной физики, решаемая также в рамках некоторых приближений. Предположим теперь, что мы знаем волновые функции электронов ионного остова, но, количество валентных электронов остаётся огромным. Поэтому необходимы дальнейшие упрощения.

Упрощение 2. Так как масса ионного остова в тысячи раз больше массы электронов (соответственно, как правило, частота колебаний ионов »10¹³ Гц, частота колебаний электронов »10¹⁵ Гц). В результате «быстрые» электроны практически мгновенно откликаются на движения атомов, а ионы чувствуют только усреднённый по времени адиабатический потенциал, создаваемый электронами. В результате гамильтониан 3.1 в приближение Борна-Оппенгеймера или адиабатическом приближении записывается в виде трёх отдельных членов –

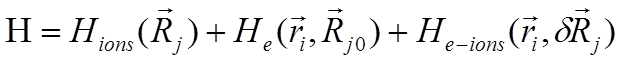   3.2

Первый член – гамильтониан, описывающий движения ионов, второй член – гамильтониан электронов, а ионы при этом «заморожены» в положении равновесия, третий член описывает взаимодействие электронов с ионными остовами (электрон-фононное взаимодействие). Обоснованность данного упрощения и некоторые эффекты, которые не вписываются в рамки адиабатического приближения, будет обсуждаться позднее.

Выпишем интересующий нас второй член гамильтониана 3.2:

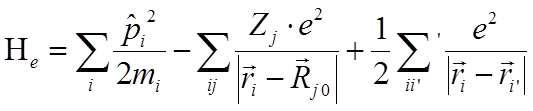      3.3

Не смотря на сделанные упрощения, число переменных в гамильтониане остаётся большим. При этом самое проблемное – это третье слагаемое гамильтониана, описывающее взаимодействие электронов, не относящихся к ионному остову (электрон-электронное взаимодействие). Осталось сделать последнее, очень радикальное приближение, которое называется приближением среднего поля, или одноэлектронным приближением. Суть его заключается в том, что каждый электрон движется в усреднённом периодическом поле, который создают ионные остовы и оставшиеся валентные электроны. Некоторые эффекты, выходящие за рамки данного приближения, будут обсуждены позже, а эффекты электрон-электронного взаимодействия обсуждаются в книге [3.5]. В рамках одноэлектронного приближения, уравнение Шредингера выглядит следующим образом:

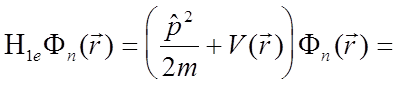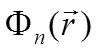e_n      3.4

Здесь – V(r) – усреднённый потенциал – периодический, с периодом кристаллической решётки (напомним, что найти его – отдельная сложная квантово-механическая задача). Фактически, нахождение собственных функций и собственных значений e_n уравнения 3.4 это решение линейного дифференциального уравнения второго порядка (вспомним вид оператора импульса) с периодическим коэффициентом при искомой функции. Как часто бывает, уравнение такого вида (без всякого практического приложения, только из интереса к абстрактной математике) было решено Матье и Флоке еще в 19 веке [3.6]. Блох решил это уравнение в общем виде именно в приложении к нахождению волновых функций и энергии электронов в кристаллах (Bloch F., Zs. Phys., v.52, p.555, 1928). Использую трансляционную симметрия кристалла (периодичность потенциала V), можно показать, что если функция  является решением уравнения 3.4, то и любая функция  (где  - любой вектор трансляции) также является решением этого уравнения. В силу линейности уравнения 3.4, решения могут различаться только на константу: . Если константа по модулю отличается от единицы, то при трансляции в нужную сторону амплитуда функции f все время возрастает. Вспомним, что квадрат модуля функции f пропорционален вероятности нахождения частицы в данной точке (физическая суть волновой функции). Интеграл квадрата модуля f по всему пространству должен быть нормирован не единицу, что невозможно сделать в данном случае. Значит, такое решение не имеет физического смысла, в квантовой механике это соответствует не стационарным решениям, собственное значение такой функции комплексно и попадает в область запрещённых энергий – запрещённую зону. Впервые, к выводу о существовании зон пришёл Стрэтт (Strutt M.J.O., Ann. Phys., v.84, p. 485, 1927).