Химическое равновесие и необратимая реакция в открытой системе. Газовая хроматография: Методическое пособие, страница 10

Приложение 1

Реакция в открытой системе при постоянном давлении.

              Будем использовать следующие обозначения:

Сим-вол	Величина	Связь с другими величинами	Размер-ность
Vр	Объём реактора		л
C0А, CА	Концентрация реагента на входе и выходе реактора		моль/л
ni	Стехиометрический коэффициент	Знак: для реагента (–), для продукта (+)
W	Скорость реакции		(моль/л)×с-1
u0 и  u	Объёмная скорость на входе и выходе реактора		л/с
n	Число молей		моль
и	Потоки реагента А на входе и выходе реактора		моль/с
x	Степень превращения реагента А		Безразмер-ная величина
	Время контакта		c

I. Реактор полного смешения.

Рассмотрим несколько примеров, начиная с наиболее простых.

Пример 1. Реакция первого порядка без изменения общего числа частиц А ¾® В.

Для реакции в закрытой системе кинетическое уравнение имеет вид

.

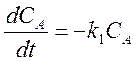Если реакция протекает в открытой системе в проточном реакторе полного смешения, то в уравнение необходимо добавить члены, описывающие изменение концентрации вещества за счёт его втекания и вытекания.

.

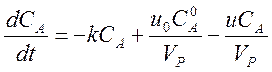Поскольку для реакции без изменения числа частиц u = u₀, в стационарном состоянии получаем соотношение

          ,                           

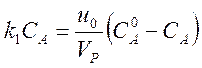из которого легко найти стационарную концентрацию С_А. В данном примере при протекании реакции не происходит изменения объёма. Поэтому степень превращения х может быть найдена, как .

Пример 2.

Реакция второго порядка без изменения числа частиц 2А ¾® C + D.

В стационарном состоянии те же соображения приводят к уравнению

.

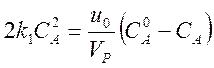Пример 3. Реакция c изменением числа частиц.

Рассмотрим общий случай, когда реакция произвольного порядка, в которой одним из реагентов является вещество А, протекает в реакторе полного смешения и число частиц не остаётся постоянным. При этом u¹u₀ и , поскольку концентрация реагента изменяется не только из-за его расходования, но и из-за разбавления продуктами реакции. Оказывается, что в этих условиях более простые соотношения получаются не для концентраций, а для потоков частиц на входе и выходе химического реактора.

В закрытой системе скорость любой химической реакции, по определению равна

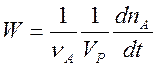     .                                   (1)

Отсюда

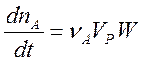.                            (2)

Для реакции в открытой системе в реакторе полного смешения

                                                                          [моль/с]

 

                                                              [л/с]

уравнение (2) необходимо дополнить членами, описывающими изменение количества вещества А в реакторе за счёт его втекания и вытекания.

.

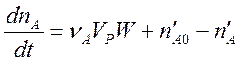В стационарном случае

.

Это уравнение имеет ясный смысл: разность потоков реагента А на входе и выходе реактора равна скорости его химического превращения во всём объёме реактора.

Вводя степень превращения вещества А, как , получаем

.

Поскольку , а , последнее равенство можно записать также в виде

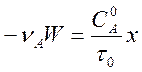,                                    (3)

где  – время контакта, а  есть функция степени превращения. Это соотношение справедливо в общем случае. В некоторых случаях нам будет удобно представлять его в виде

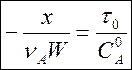                               (3а)

Пример 4. Реакция первого порядка, протекающая с увеличением числа частиц  А ¾® В + С.

Подставляя в равенство (3) n_А = –1 имеем

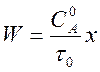.                                        (4)

Теперь нужно выразить скорость реакции W через степень превращения, используя закон действующих масс.

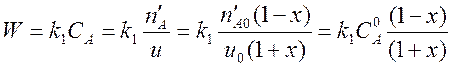.                    (5)

Подставляя выражение (5) в уравнение (4), получаем квадратное уравнение для вычисления х.

.

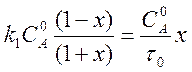Его решение не вызывает затруднения.

При выводе этого уравнения мы учли, что  и . Если первое из этих двух соотношений является следствием определения степени превращения х, то второе требует пояснения.