Фотоэлектромагнитный комплекс методов определения рекомбинационно-диффузионных параметров носителей заряда в эпитаксиальных плёнках кадмий-ртуть-теллур Р-типа, страница 6

где  − собственная фотопроводимость, которая пропорциональна общему числу ННЗ в плёнке;  - магнито-диффузионная составляющая [28], связанная с диффузией неоднородно распределённых по толщине образца неравновесных электронов.

При отсутствии тянущего поля (E_x=0) напряжение  совпадает с напряжением ФМЭ: . В работе [27] приведены аналитические выражения для  и , которые имеют следующий вид:

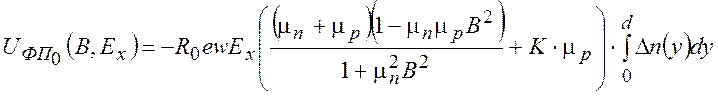,            (13)

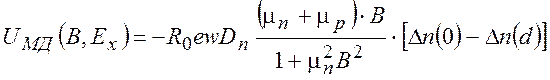.                          (14)

Компоненты (13) и (14), в которых  − профиль концентрации неравновесных электронов в центральной однородной по х области плёнки, при постоянной температуре (Т = 77 К), изменяются в стационарных  полях и зависят от геометрических размеров плёнки: w, с и d (см. Рис. 1); от темнового сопротивления R₀ (для р-КРТ, т.к.  ), от параметров падающего на плёнку излучения: ; от параметров основных носителей заряда:  и ; от параметров неосновных носителей заряда:  и К; а также от ,  и .

При подстановке в выражения (13) и (14) , ,  и К, определённые ранее описанными методами, геометрических размеров: w, d, с и вычисленного значения , ФП в геометрии Фойгта и ФМЭ будут зависеть только от , , ,  и .

Подгонка теоретических выражений (13) и (14) для ФП в геометрии Фойгта и ФМЭ под экспериментальные данные выполнялась методом наименьших квадратов с минимизацией функции , которая имеет вид:

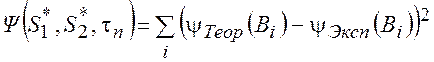,                                 (15)

где 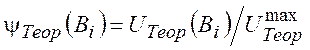, ,  и  − теоретические и экспериментальные значения ФМЭ или ФП при индукции магнитного поля B_i, 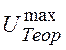 и  − наибольшие теоретические и экспериментальные значения ФМЭ или ФП. Отношение сигналов используется для того, чтобы исключить  и , которые точно не известны. Такой приём используется при измерении фотоэлектромагнитных эффектов [29]. Подгонка осуществлялась методом наименьших квадратов с использованием методов многомерного поиска, а именно, способа случайного поиска в сочетании со способом Хука-Дживса [9].

            Точность полученных значений времени жизни неосновных электронов и скоростей поверхностной рекомбинации можно оценить по статистическому разбросу в полученных данных по результатам многочисленных (сто и более) подгонок с вычислением среднего значения и доверительного интервала. Из соответствия теоретических выражений (13), (14) и экспериментальных данных были определены рекомбинационно-диффузионные параметры структуры: S_1эфф =  (37±7)  м/с, S_2эфф =  (38±7)  м/с, t_n =  (11±1)  нс [27].

Закдючение

            В работе для эпитаксиальных плёнок МЛЭ p-КРТ c x ≈ 0,2 при азотных температурах предложен фотоэлектромагнитный комплекс методов диагностики рекомбинационно-диффузионных параметров носителей заряда, таких, как: μ_n, τ_n, τ_p, K, S₁^*, S₂^*, C_n, C_p, N_t и E_t. Комплекс включает такие методы, как «спектр подвижности» в сочетании с так называемой многозонной подгонкой, ФП для геометрий Фарадея и Фойгта, а также ФМЭ.

            Методом «спектра подвижности» в сочетании с так называемой многозонной подгонкой определялись с погрешностью не более ±15% подвижность μ_p и концентрация p основных носителей заряда. Из анализа ФП в геометрии Фарадея были определены μ_n и K; оценены C_n и C_p, N_t и E_t. Относительная погрешность определения μ_n и K для температур до 100 К составила 2% и 17%, соответственно.

            Методом ФП в геометрии Фойгта и ФМЭ были определены τ_n, S₁^* и S₂^* с погрешностью 10% и 20%, соответственно.

Литература

1.  Рогальский А. Инфракрасные детекторы/ Пер. с англ. – Новосибирск.: Наука, 2003. 636 с.

2.  Костюченко В.Я. Влияние стационарных скрещенных электрических и магнитных полей на фотогенерированные носители заряда в эпитаксиальных плёнках кадмий-ртуть-теллур p-типа (Обзор)// Вестник НГУ. Серия: Физика. 2010. Т. 5. вып. 1. С. 66-81.

3.  Протасов Д.Ю., Костюченко В.Я. Эффективные темп оптической генерации и скорости поверхностной рекомбинации носителей заряда в варизонных плёночных фотоприёмных структурах р-КРТ МЛЭ // Автометрия. 2009. Т. 45, вып. 4. С. 103−108.

4.  Госсорг Ж. Инфракрасная термография. Основы, техника, применение//Пер. с франц. М.: Мир, 1988. 416 с.

5.  Beck W.A., Anderson J.R. Determination of electrical transport properties using a novel magnetic field-dependent Hall technique// J. Appl. Phys. 1987. Vol. 62. P. 541 - 554.