Фотоэлектромагнитный комплекс методов определения рекомбинационно-диффузионных параметров носителей заряда в эпитаксиальных плёнках кадмий-ртуть-теллур Р-типа, страница 5

В интервале температуры 125÷300 К, когда наблюдается смешанная проводимость, значение , определённое методом «спектра подвижности», с хорошей точностью (менее 5%) совпадают с , определённой с помощью подгонки теоретических выражений для ФП в геометрии Фарадея [19] под экспериментальные данные.

Как видно из рис. 6, ФП выходит на насыщение уже при 1,5¸2 Тл и из (7) можно найти коэффициент пропорциональности К:

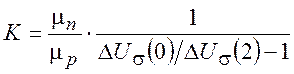.                                             (9)

Абсолютная погрешность коэффициента К рассчитывается по выражению:

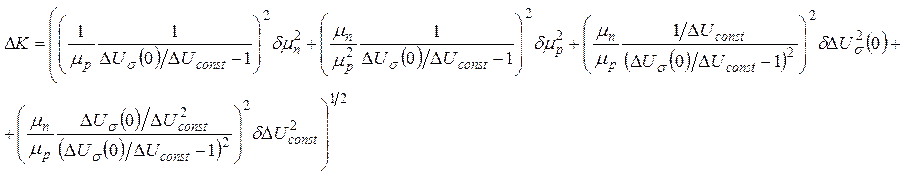(10)

Подвижность неосновных электронов в МЛЭ p-КРТ при Т = 77 К приведена выше, а значение коэффициента К составляет 5÷30 [20]. Поэтому проведем расчет по формуле (9) при следующих значениях параметров: μ_n=6 м²/(В·с), μ_p = 0,03 м²/(В·с), ΔU_σ(0) = 1 и ΔU_const = 0,08, что дает величину К равную 17,4. Погрешности нахождения этих величин описаны выше: δμ_n./μ_n = 1 %, δμ_p./μ_p = 15 % и δΔU_σ(0)  =  δΔU_sat = 0,5 %. Тогда расчет по формуле (10) дает значение ΔK = 2,9, или ΔK/K = 17%.

В работе [20] показано, что К можно представить виде:

.                                                          (11)

Сравнивая выражения (9) и (11), можно определить :

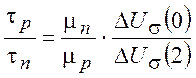.                                                       (12)

Экспериментальные значения  интерпретировались аналитическими выражениями [21], описывающими значения  и  в р-КРТ с учётом таких механизмов рекомбинации, как излучательного, Оже-7 и Шокли-Рида-Холла. Параметры ,   и  использовались в качестве подгоночных, а для концентрации РЦ было предложено выражение:

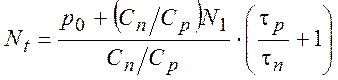,                                 (13)

где  - эффективная плотность состояний электронов в зоне проводимости, приведённая к уровню РЦ.

Были определены указанным способом  мэВ,  м⁻³/с,  м⁻³/с. Энергия  лежит близко к середине запрещённой зоны, что согласуется с опубликованными данными [22, 23]. Концентрация РЦ N_t ≈ 10¹⁹ м⁻³ и не зависела от  в интервале  м⁻³.

Как отмечалось ранее, применение классических методов исследования РЦ в p-КРТ с х » 0,2 затруднено, поэтому является актуальным развитие метода ФП в геометрии Фарадея для оценки значений N_t, C_n, C_p и E_t.

Поглощение излучения в варизонной области

При измерении ФП и ФМЭ ННЗ генерировались ИК-светодиодом с длиной волны λ = 0,94 мкм. Для расчета коэффициента поглощения использовались выражения, полученные в работе [24]. Значение коэффициента поглощения для x  0,22 составляет 2×10⁶ м^-1, и возрастает при увеличении х в плёнке до 0,4÷0,5. В варизонной области коэффициент поглощения излучения равен среднему значению: 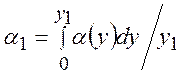. Оценить погрешность вычисленного коэффициента поглощения достаточно сложно. Однако для этого можно использовать результаты работы [25]. В этой работе коэффициент поглощения использовался как дополнительный подгоночный параметр при анализе данных ФМЭ в p-КРТ с х  0,22, и для длины волны 1,3 мкм при температуре 77 К его отличие от значения, рассчитанного согласно [24], не превышало 5%.

Методы определения времени жизни неосновных носителей заряда и скорости поверхностной рекомбинации

Предлагается для плёнок р-КРТ определять ,  и  подгонкой теоретичсеких кривых ФП в геометрии Фойгта и ФМЭ к экспериментальным данным.

Методы измерения времени жизни ННЗ в полупроводниках можно разделить на кинетические и стационарные [26]. Применение метода релаксации ФП в р-КРТ затруднено, так как значение времени жизни мало (от нескольких наносекунд до десятков наносекунд [21]). Это накладывает ограничения на длительность фронтов импульсов излучения, которые должны быть много меньше времени жизни ННЗ. Метод стационарной ФП, который применим для полупроводников с малыми значениями времени жизни носителей заряда, не требует применения сложной аппаратуры (источника оптической накачки с малым временем спада импульса и «быстрой» электроники). Для получения более достоверной информации о значениях ,  и  в плёнках р-КРТ с х ~ 0,2 анализировались совместно магнитополевые зависимости ФП и ФМЭ.

Сигнал ФП в геометрии Фойгта можно представить в виде [27]:

,                     (12)