Фотоэлектромагнитный комплекс методов определения рекомбинационно-диффузионных параметров носителей заряда в эпитаксиальных плёнках кадмий-ртуть-теллур Р-типа, страница 2

Для проведения измерений методом фотолитографии формировалась классическая холловская структура длиной 10 мм и шириной w = 1 мм (рис. 1). Меза-травление проводилось в 0,25% растворе Br₂:HBr. Затем структура укреплялась индием к сапфировой подложке и к структуре изготавливались омические индиевые контакты.

Геометрия образца и схема измерения ФП в геометрии Фарадея показаны на рис. 1. Через контакты 1, 2 образца пропускался постоянный ток в режиме генератора тока. Без освещения плёнки измерялись магнитосопротивление с контактов 3, 5 или 4, 6; эффект Холла - с контактов 3, 4 или 5, 6. Для измерения сигналов ФП и ФМЭ образец освещался через диафрагму шириной 1 мм. Свет попадал на центральную часть образца (заштрихована), за счёт чего исключалось попадание света на контакты, а фотогенерированные ННЗ не достигали контактов. На рис. 1 указаны условия, когда между контактами 3, 5 или 4, 6 измерялась ФП в геометрии Фарадея. При повороте держателя с образцом на угол , так что  и , с контактов 4, 6 или 3, 5 при прохождении тока измерялся сигнал ФП в геометрии Фойгта, а при отсутствии тока – сигнал ФМЭ.

На рис. 2 приводится схема экспериментальной установки. Образец 1 в криостате 2 помещался между полюсами электромагнита 3. Индукция магнитного поля изменялась от 0 до 2 Тл, ее значение измерялось при помощи датчика Холла 4, питающегося от источника тока 5. При измерении эффекта Холла, магнитосопротивления и ФП в магнитном поле для двух геометрий через образец пропускался постоянный ток Iот источника 7. При измерении ФП (положение 2 коммутатора К) образец освещался светодиодом 10 (λ~0,94 мкм), питающимся от генератора переменного напряжения 11 на частоте f=330 Гц. Измеряемый сигнал регистрировался с помощью фазочувствительного нановольтметра 12 на опорной частоте генератора 11. Температура образца регулировалась в диапазоне от 77 К до 300 К с помощью нагревателя 8 и стабилизатора температуры 9. Сигналы с образца и с датчика Холла регистрировались компьютером 6.

Методы определения параметров основных носителей заряда.

В основу классического метода определения ,  положен эффект Холла и магнитосопротивления. Для повышения точности  и  экспериментальные магнитополевые зависимости эффекта Холла и магнитосопротивления анализировались методом «спектра подвижности» и так называемой многозонной подгонкой.

На рис. 3 приводятся экспериментальные магнитополевые зависимости коэффициента Холла R_H (сплошная линия) и относительной проводимости в магнитном поле  (пунктирная линия) при Т = 77 К для образца p-КРТ с х = 0,223. Как видно из рис. 3, коэффициент Холла уменьшается при увеличении магнитного поля до В = 0,75 Тл практически линейно. При дальнейшем увеличении магнитного поля скорость убывания R_H падает. Относительная проводимость при увеличении В изменяется пропорционально B² (см. Рис. 3), затем зависимость становится более линейной. Такое поведение кривых связано с наличием двух типов дырок – лёгких и тяжёлых, причём подвижность лёгких дырок может в несколько десятков раз превышать подвижность тяжелых дырок.

Концентрации и подвижности различных типов носителей заряда определялись подгонкой теоретических выражений под экспериментальные данные для эффекта Холла и магнитосопротивления. Подгонка выполнялась методом наименьших квадратов с минимизацией функции Yспособом Хука-Дживса [9]. При обработке результатов измерений эффекта Холла и магнитосопротивления минимизируемая функция Y в общем случае зависела от шести переменных: концентрации n и подвижности  электронов; концентраций  и , подвижностей  и  тяжёлых и лёгких дырок, соответственно. Минимизируемая функция в этом случае имела вид:

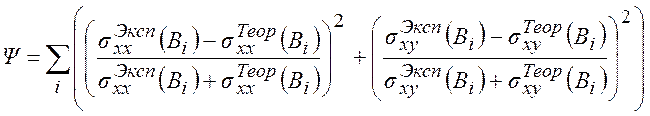,                (1)

где магнитополевые зависимости компонент тензора проводимости рассчитывались по формулам:

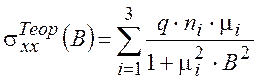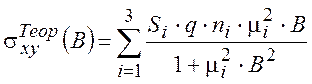,          ,                  (2)

где S_i равно +1 (для дырок) и -1 (для электронов). Подобные уравнения справедливы при времени релаксации по импульсу, независящем от энергии носителей заряда. В этом случае величина Холл-фактора равна точно 1. Так как концентрация тяжелых дырок более чем на два порядка превышает концентрацию легких дырок, то тяжелые дырки дают основной вклад в компоненты тензора проводимости (2). Величина Холл-фактора для p-Hg_0.8Cd_0.2Te с концентрацией тяжелых дырок ~1×10²² м^-3 рассчитана в работе [10] путем самосогласованного решения кинетического уравнения Каданова-Бейма, и при Т = 77 К составляет для тяжелых дырок 1,02, а для легких – 1,78. Поэтому использование простых уравнений (2) даёт малую погрешность при определении подвижности и концентрации тяжелых дырок.