Формулировка принципа относительности Галилея. Задача 2-х тел. Приведенная масса. Движение тел с переменной массой

Лекция 4

Формулировка принципа относительности Галилея состоит в утверждении, что все инерциальные системы отсчета равноправны. Это означает, что все физические опыты, выполняемые в инерциальных системах, отсчета приводят к одинаковым результатам.

Из выражения II-го закона Ньютона следует, что он не выполняется в любой системе отсчета. В самом деле, ускорение имеет различные значения в разных системах, движущихся ускоренно друг относительно друга, тогда как сила является функцией взаимного расстояния и относительных скоростей взаимодействующих частиц, которые в нерелятивистской механике  не зависят от выбора системы отсчета.

Рассмотрим две инерциальные системы отсчета  К и .  движется со скоростью относительно К. Необходимо найти закон преобразования координат при переходе из одной системы отсчета в другую, т.е определить зависимости набора  от . Решение задачи выражается в формулах преобразования Галилея.

                                           (1)

Первая из приведенных формул означает, что время абсолютно. Другими словами секунда, измеренная в одной системе равна секунде, измеренной по приборам другой системы отсчета. Вторая формула кажется очевидной. Физический смысл ее состоит также в инвариантности (неизменности) длин, измеренных в разных системах отсчета. Процедура измерения интервалов времени и длин была подвергнута строгому физическому обоснованию в релятивистской специальной теории относительности. Получены преобразования Лоренца координат, времени, скоростей которые в предельном случае малых нерелятивистских скоростей переходят в преобразования Галилея.

            Дифференцирование соотношений (1) позволяет получить преобразования скоростей при переходе из одной системы отсчета в другую. Во-первых ,

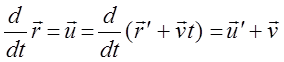, при условии, что . Вычисление следующей производной дает: 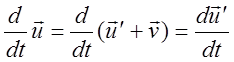, т.е . Если учесть, что,  т.к. . Окончательно:

.

Вид II – го закона Ньютона оказался неизменным.  Это означает, что результаты физических опытов, описываемых уравнениями Ньютоновской механики должны быть одинаковы в различных инерциальных системах. 

Задача 2-х тел. Приведенная масса.

Рассмотрим движение 2-х частиц взаимодействующих друг с другом в отсутствие других, внешних сил. Например, хорошим приближением такого движения является движение Земли в поле тяготения Солнца, либо движение орбитального электрона в кулоновском поле ядра. Напишем уравнения движения частиц. Считая  радиус векторами частиц в выбранной системе отсчета, имеем:

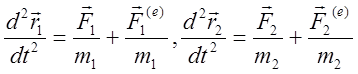                             (6)

Полагая  - отсутствие внешних сил и - III –й закон Ньютона, вычитая из второго уравнения первое получаем:

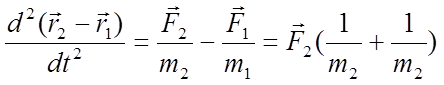                           (7)

Вводя  и, обозначая 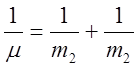, получаем окончательно:

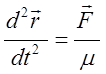 или                                                 (8)

Формально задача свелась к интегрированию единственного уравнения движения частицы массы  под действием силы .  - называется приведенной массой.

Движение центра масс системы материальных точек.

Ранее было показано, что 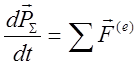- изменение импульса системы зависит только от внешних сил. Приведенное уравнение справедливо в наиболее общем случае, в том числе для описания движения тел с переменной массой . После введения полной массы системы 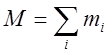и скорости центра масс 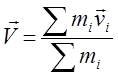, легко переписать уравнение для  в ви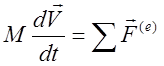де: , где - ускорение центра масс. Точкой приложения результирующей внешних сил является центр масс.

Движение тел с переменной массой.

            Характерным примером движения тела с переменной массой является движение реактивного снаряда (ракеты) под действием истекающих из двигателя газов. Интерес к такого вида устройствам повысился в прошлом веке в связи с возможностью достижения подобными аппаратами космических скоростей, по порядку величины 10 км/c.

Точное решение модельных уравнений движения было получено Мещерским И.В.. Частный случай решения известен как формула Циолковского К.Э.

Рассмотрим движение ракеты с «сухой» массой . На ракете установлен топливный бак с  порциями топлива по  каждая. Будем считать, что каждая порция топлива, сгорая мгновенно, вылетает со скоростью  относительно ракеты. Последние предположения являются модельными, однако в этом случае удается получить решения уравнений движения в квадратурах.

Принцип ускорения ракеты прост. Газы, истекая из двигателя, уносят некоторый секундный импульс. Тот же импульс получает ракета с остатками топлива, будучи вместе с газами замкнутой системой. Предполагается, что внешних сил нет.