Формулировка принципа относительности Галилея. Задача 2-х тел. Приведенная масса. Движение тел с переменной массой, страница 2

Возникает вопрос как эффективнее сжигать топливо – либо все порции сразу, либо по очереди одну за другой.

Рассчитаем точно II – й режим. Пусть космический кочегар – простой парень из Напервилля близ Чикаго Дж. Стинг забрасывает в топку «Сатурна» одну лопату угля за другой. После сжигания первой лопаты  - скорость «Сатурна»,  - скорость истекающих газов в лабораторной системе отсчета (в дальнейшем л.с.). В наших предположениях - . Запишем закон сохранения импульса для замкнутой системы «ракета – газы».

                                   (9)

После исключения скорости и несложных преобразований находим:

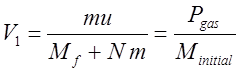                                        (10)

где - импульс истекающих газов, - масса «Сатурна» до истечения первой порции. По смыслу  - является приращением скорости. Аналогично, после сжигания 2-й лопаты:

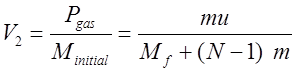,                                 (11)

-й:

.                                        

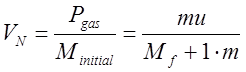Полная скорость после сжигания всего уголька:

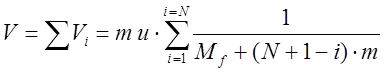                   (12)

Всего в сумме слагаемых.

Рассмотрим I – й режим. Топливо сжигается все сразу. Все лопат одновременно заброшены в топку, истечение происходит со скоростью относительно ракеты. Подставляя в (10) , а  находим:

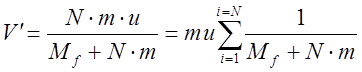                       (13)

Все слагаемые суммы (13), за исключением первого, меньше слагаемых суммы (12), следовательно . Сжигать уголек порциями, не торопясь, более эффективно. Отметим, что при единовременном сжигании , скорость «Сатурна» меньше скорости истекающих газов.

В двигателе реальной ракеты топливо сжигается вовсе не порциями, из двигателей истекает непрерывный поток высокотемпературных газов. Перепишем соотношение (11) в дифференциальной форме, вводя вместо конечного изменения  массы его бесконечно малый аналог . При этом масса ракеты вместе с остатком топлива в некоторый момент времени - . Тогда (11) перепишется:

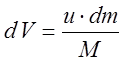                                                  (14)

Интегрируя:

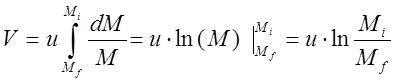                 (15)

В (15)  соответственно «стартовая» и «сухая» массы ракеты. Как правило известна. Нетрудно определить  для достижения заданной скорости:

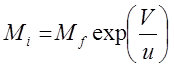                                          (16)

Последние две формулы называются формулами Циолковского.

            Дифференциальное уравнение (14), которое дает решение (15) можно переписать в виде: . Оно отражает ситуацию, когда внешние силы отсутствуют. Допустим, что существуют внешняя сила , которая за бесконечно малый интервал времени сообщает ракете приращение импульса . В этом случае правая часть уравнения станет ненулевой:  , или, в векторной форме:

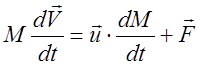                          (17)

(17) называется уравнением Мещерского.

Проведем некоторые оценки по формуле Циолковского.

                                                                                               Таблица 1

	1	2	3	4	5	6	7	8	9	10
	2.72	7.39	20.1	54.6	148	403	1100	2980	8100	22000

1. Космический корабль «Союз» имеет полную стартовую массу т.. Выводит на околоземную орбиту полезную массу т. Будем считать, что I-я космическая скорость на низкой орбите. Тогда скорость истечения: . Это «эффективная» скорость истечения. Реальная скорость газов на срезе сопла двигателей выше - . Однако к полезной массе, выводимой на орбиту следует добавить массу «сухой» ракеты (около 30т), которая, однако сбрасывается на разгонном участке ступенями.
2. Оценим массу ракеты, необходимую для получения II-й космической скорости 11,2  при скорости истечения 2,2 . . Иначе говоря, чтобы отправить на бесконечность, на расстояния много большие радиуса Земли, тонну полезного груза необходимо сжечь 150 тонн топлива.
3. Для путешествия на Марс за неделю необходима скорость . При скорости истечения продуктов сгорания химических топлив на уровне 2,2 2,5  потребуется фантастическая стартовая масса, превышающая полезную массу в раз. Очевидно, что такие параметры ныне недостижимы. Если использовать ядерный реактор для нагревания водорода, то можно поднять скорость истечения до 9. Тогда на полета на Марс потребовалось бы относительно немного топлива на каждую единицу массы полезного груза - . Самая массивная из существующих ныне ракет – «Сатурн-5» имеет стартовую массу 3,5 тысячи тонн.