Лекция 4

![]() Термы атомов
Термы атомов
Энергия атома определяется:
![]()
![]() квантовыми
числами отдельных электронов n и
квантовыми
числами отдельных электронов n и ![]() (взаимодействие электронов с «ядром» с эффективным
зарядом);
(взаимодействие электронов с «ядром» с эффективным
зарядом);
полным орбитальным моментом L и спином S атома (электростатическое взаимодействие электронов между собой, не учтенное в приближении центрально симметричного поля (Собельман, 38));
![]() полным моментом атома J (спин-орбитальное
взаимодействие).
полным моментом атома J (спин-орбитальное
взаимодействие).
![]()
Как
определить L, S и J при известных из одноэлектронного приближения
![]() ? Это
квантовомеханическая задача сложения моментов, которую удобнее и нагляднее
решать методом сложения проекций
? Это
квантовомеханическая задача сложения моментов, которую удобнее и нагляднее
решать методом сложения проекций ![]() и
и ![]() .
.
проекция спина +1/2 обозначим стрелкой вверх, -1/2 - стрелкой вниз.
отрицательные значения проекций полных орбитального и спинового моментов ML и MS опускаем
учитываем принцип Паули
составляем таблицу
Таблица 5.
![]() Для
незаполненной подоболочки np2
Для
незаполненной подоболочки np2
|
|
|
|||||
|
+1 |
|
|
|
|
|
|
|
0 |
|
|
|
|||
|
-1 |
|
|
||||
|
Ms |
1 |
1 |
0 |
0 |
0 |
0 |
|
ML |
1 |
0 |
1 |
0 |
2 |
0 |
1S, 1D и 3P термы (сокращенно 1S D 3P)
![]() Для
незаполненной подоболочки np3
Для
незаполненной подоболочки np3
|
me |
ms |
||||||
|
+1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
||
|
Ms |
3/2 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
|
ML |
0 |
0 |
0 |
0 |
2 |
1 |
1 |
2P, 2D, и 4S термы
![]() Очевидно, что полностью заполненная подоболочка имеет L = 0
и S = 0 .
Очевидно, что полностью заполненная подоболочка имеет L = 0
и S = 0 .
![]()
Энергетическое распределение термов регламентируется правилом Хунда:
1. Наименьшей энергией обладает терм с максимальным значением спина S при данной электронной конфигурации и максимально возможным при этом Smax значении L.
2.
Для основного (нормального)
терма: J = ![]() , если подоболочка заполнена менее чем наполовину, и J = L + S
в остальных случаях.
, если подоболочка заполнена менее чем наполовину, и J = L + S
в остальных случаях.
Следовательно, имеем следующую последовательность термов: при nр2: 3P0, 1D2, 1S0; при np3: 4S3/2 , 2D5/2, 3/2 , 2P3/2, 1/2 .
· Физические основы правила Хунда легко понять, если представить, например, два электрона на одной орбите. Электростатическое отталкивание будет стремиться заставить их вращаться в одном направлении. Если они вращаются навстречу, то будут часто встречаться, т.е. средняя электростатическая энергия будет больше. Таким образом, стремление к максимуму L можно понять из простейшей классической аналогии.
· Причины сильного взаимодействия спинов имеют чисто квантовый характер и не имеют классической аналогии. Действительно, прямое взаимодействие спиновых магнитных моментов слишком мало. Дело заключается в том, что полная волновая функция должна иметь определенную симметрию, а именно, должна быть антисимметрична. Изменение полного спина влечет за собой изменение симметрии спиновой волновой функции и, как следствие, требует изменения симметрии координатной части волновой функции, т.е. изменения электронной конфигурации атома, а, следовательно, и изменения электростатического потенциала атома. Именно в этом смысле говорится об электростатическом взаимодействии спинов электронов.
![]()
.
![]() Переход называется разрешенным, если в величине Vij
отличен от нуля дипольный член разложения. В этом случае вероятности перехода
максимальны Vij ~ dij . Если дипольный момент
перехода dij равен нулю, то переход называют запрещенным.
Переход называется разрешенным, если в величине Vij
отличен от нуля дипольный член разложения. В этом случае вероятности перехода
максимальны Vij ~ dij . Если дипольный момент
перехода dij равен нулю, то переход называют запрещенным.
![]()
![]() ,
,
кроме случая J1 = 0 и J 2 = 0.
![]() Спектр атома водорода
Спектр атома водорода
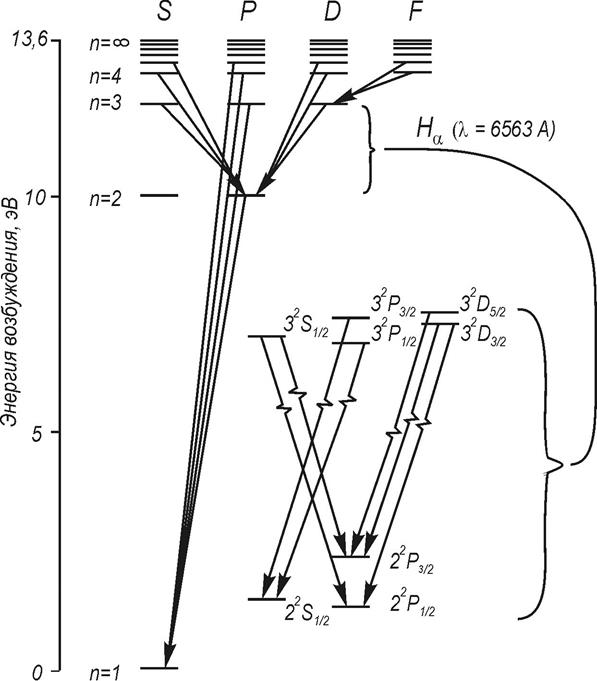
На рис. 3 показаны энергетические уровни и разрешенные переходы в атоме водорода.
![]() Частота перехода (без учета тонкой структуры)
Частота перехода (без учета тонкой структуры)
Частота перехода (без учета тонкой структуры):
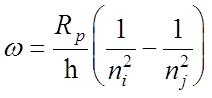
Правила отбора: ![]()
![]()
![]() (кроме
J1=0 и J2=0).
(кроме
J1=0 и J2=0).
1. Ультрафиолетовая серия Лаймана:
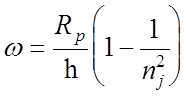 , где nj = 2,
3...
, где nj = 2,
3...
![]()
2. Серия Бальмера (видимая область спектра):
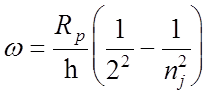 , где nj = 3,
4, 5...
, где nj = 3,
4, 5...
![]() = 6563
= 6563 ![]() (nj = 3),
(nj = 3),
![]() = 4861
= 4861 ![]() (nj = 4),
(nj = 4),
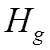 = 4340
= 4340 ![]() (nj = 5).
(nj = 5).
3. Инфракрасная серия Пашена:
![]()
![]()
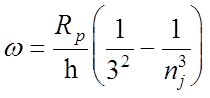 , где nj = 4,5,6...,
, где nj = 4,5,6...,
![]() 1 = 18751
1 = 18751 ![]() , (nj = 4)
, (nj = 4)
![]() Более
подробно (на рис. 3) представлены уровни энергии с n = 3.
Учет тонкой структуры и лэмбовского сдвига приводит к формированию семи линий
Более
подробно (на рис. 3) представлены уровни энергии с n = 3.
Учет тонкой структуры и лэмбовского сдвига приводит к формированию семи линий
![]()
![]()
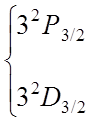 >
> ![]()
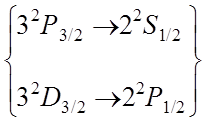
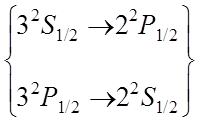
![]()
Фигурной скобкой объединены термы, энергия которых отличается только на малую величину лембовского сдвига.
![]() Спектры щелочных металлов
Спектры щелочных металлов
![]() один 1s-электрон в верхней подоболочке, спектр существенно
отличаются от спектра водорода (см. диаграмму):
один 1s-электрон в верхней подоболочке, спектр существенно
отличаются от спектра водорода (см. диаграмму):
![]() снято вырождение
по орбитальному моменту
снято вырождение
по орбитальному моменту ![]() внешнего электрона.
внешнего электрона.
![]() энергия уровня зависит от
энергия уровня зависит от ![]() настолько
сильно, что нельзя уже говорить о расщеплении уровня с данным n. Скорее,
уровни с заданным
настолько
сильно, что нельзя уже говорить о расщеплении уровня с данным n. Скорее,
уровни с заданным ![]() описываются водородоподобно (см. раздел 1.1) с эффективным квантовым
числом n*.
описываются водородоподобно (см. раздел 1.1) с эффективным квантовым
числом n*.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.