3.2. Уширение спектральных линий
Из (142) мы получаем, что время жизни атомной системы в состоянии j относительно перехода в нижнее состояние f определяется выражением
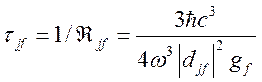 . (144)
. (144)
Очевидно, что полное время жизни на уровне j определяется полной вероятностью переходов на все ниже лежащие уровни (f < j)
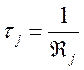 ,
(145)
,
(145)
где
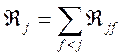 .
.
Конечное время жизни атомной системы в состоянии j определяет энергетическую ширину уровня j
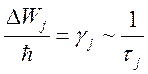 .
(146)
.
(146)
Для поперечной электромагнитной волны интенсивность излучения
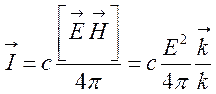 . (147)
. (147)
Спектральное распределение напряженности электрического поля излучаемой волны определяется выражениями
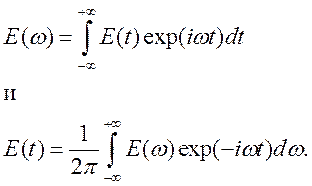 (148)
(148)
В системе отсчета атома величина электрического поля волны с учетом конечного времени жизни cостояний j и f (146) может быть записана в виде [1]
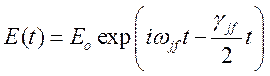 при
при ![]() (149)
(149)
и E(t) = 0 при t < 0.
Здесь ![]() — как будет показано ниже, определяет
спектральную ширину линии перехода атомной системы из состояния j в
состояние f:
— как будет показано ниже, определяет
спектральную ширину линии перехода атомной системы из состояния j в
состояние f: 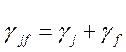 [5].
[5].
Спектральное распределение интенсивности в волне можно найти из условия [1]
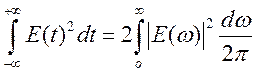 . (150)
. (150)
Откуда для мощности, излучаемой
одним атомом (молекулой) за все время в виде волн с частотами в интервале ![]() , можно получить выражение из (147) заменой
E(t) на
, можно получить выражение из (147) заменой
E(t) на ![]() , то есть
компонентами Фурье и одновременным умножением на 2
, то есть
компонентами Фурье и одновременным умножением на 2
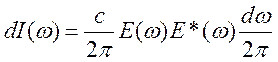 . (151)
. (151)
Если атом участвует в движении,
то в лабораторной системе отсчета нами будет регистрироваться волна с частотой,
измененной за счет эффекта Допплера: 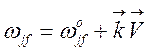 , то есть
, то есть
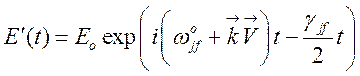 .
.
В этом случае из (148) для ![]() имеем
имеем
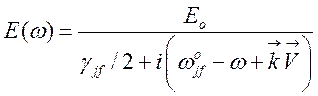
и из (151) имеем
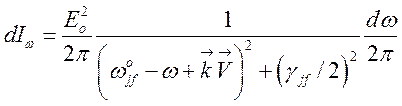 . (152)
. (152)
Перепишем выражение (151) в следующем виде [5]:
![]() , (153)
, (153)
где 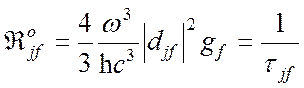 — вероятность
спонтанного перехода,
— вероятность
спонтанного перехода, ![]() — концентрация атомов в состоянии j,
— концентрация атомов в состоянии j,
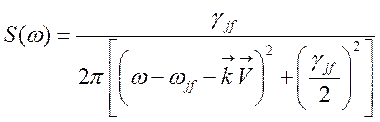
— нормированная на единицу ширина уровня.
Учитывая, что атомы участвуют в тепловом движении, спектральное распределение интенсивности будет определяться выражением
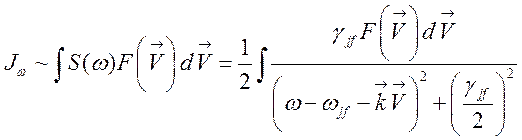 , (154)
, (154)
где F(![]() ) — функция распределения частиц по
скоростям.
) — функция распределения частиц по
скоростям.
Рассмотрим
предельный случай ![]() , что на практике означает, что
преобладает уширение линии за счет разброса скоростей. Хорошо известно, что
, что на практике означает, что
преобладает уширение линии за счет разброса скоростей. Хорошо известно, что
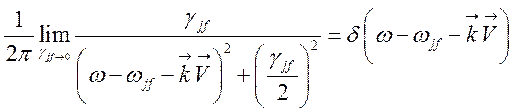 .
.
Таким образом, из (154) при ![]() получим
получим
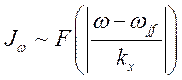 ,
(155)
,
(155)
то есть допплеровское уширение линии, в направлении оси х. Выражение (155) получено в приближении, что в течение всего времени излучения атома его скорость оставалась постоянной.
Как мы уже
отмечали в [5] собственное время жизни (146), с учетом ![]() и
и
![]() , можно записать в виде
, можно записать в виде 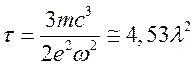 . При
. При ![]() получим
получим
![]() , то есть
, то есть ![]() сек-1. Допплеровская ширина при нормальных
условиях (
сек-1. Допплеровская ширина при нормальных
условиях (![]() см/с) и
см/с) и ![]() равна
равна ![]() , то есть в 40 раз больше естественной
ширины
, то есть в 40 раз больше естественной
ширины ![]() .
.
В другом
предельном случае уширение линии за счет ![]() оказывается
существенно больше эффектов, обусловленных разбросом скоростей. В этом случае
профиль линии описывается выражением:
оказывается
существенно больше эффектов, обусловленных разбросом скоростей. В этом случае
профиль линии описывается выражением:
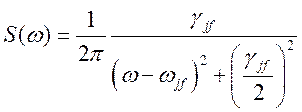 . (156)
. (156)
Данный профиль линии называют
Лоренцовским. Подобная ситуация может возникнуть обычно в двух случаях.
Во-первых, при очень низкой температуре, при которой естественная ширина линии
оказывается больше, чем допплеровское уширение или, во-вторых, при нормальной
температуре, если величина ![]() очень велика, например,
за счет столкновений, сокращающих время жизни атома в состоянии j. С
точки зрения излучаемой волны (149) обычно говорят о сбое фазы. В этом случае
имеем
очень велика, например,
за счет столкновений, сокращающих время жизни атома в состоянии j. С
точки зрения излучаемой волны (149) обычно говорят о сбое фазы. В этом случае
имеем ![]() , где
, где ![]() —
частота и сечение атомных столкновений, соответственно,
—
частота и сечение атомных столкновений, соответственно, ![]() —концентрация
атомов. Необходимо отметить, что
—концентрация
атомов. Необходимо отметить, что ![]() , если каждое столкновение
будет приводить к сбою фазы, то есть безызлучательному переходу атома из
состояний j и f в какие-то другие состояния. Однако, реально это
не всегда так. Вероятность безизлучательного перехода при столкновении может
быть и не равна единице и тогда требуется несколько столкновений, чтобы
произошел сбой фазы. В этом случае
, если каждое столкновение
будет приводить к сбою фазы, то есть безызлучательному переходу атома из
состояний j и f в какие-то другие состояния. Однако, реально это
не всегда так. Вероятность безизлучательного перехода при столкновении может
быть и не равна единице и тогда требуется несколько столкновений, чтобы
произошел сбой фазы. В этом случае ![]() , где
, где ![]() .
.
Очевидно, что при заданной температуре существует некоторая критическая плотность, при превышении которой столкновительное уширение будет превышать допплеровское. Принимая, что
![]()
при ![]() ,
, ![]() (азот при нормальных условиях) и учитывая,
что
(азот при нормальных условиях) и учитывая,
что ![]() с-1
при
с-1
при ![]() см, получим
см, получим ![]() при
при ![]() , то
есть при давлении
, то
есть при давлении ![]() . Следовательно, в условиях
рассмотренного примера при постоянной температуре увеличение
. Следовательно, в условиях
рассмотренного примера при постоянной температуре увеличение ![]() приведет к увеличению ширины линии и ее
профиль станет не допплеровским (155), а лоренцовским (156).
приведет к увеличению ширины линии и ее
профиль станет не допплеровским (155), а лоренцовским (156).
Однако, можно
рассмотреть ситуацию, когда столкновения изменяют направление и величину
скорости частицы, но при этом не влияют на излучаемую волну, то есть оставляют
неизменной фазу (или состояние атома). Будем рассматривать случай, когда
частота столкновений столь велика, что длина свободного пробега между
столкновениями ![]() меньше длины волны. Тогда набег
фазы, связанный с пространственным смещением частицы, равен
меньше длины волны. Тогда набег
фазы, связанный с пространственным смещением частицы, равен
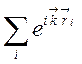 ,
,
где ![]() —
радиус-вектор смещения частицы после i-го столкновения. Учитывая, что
—
радиус-вектор смещения частицы после i-го столкновения. Учитывая, что ![]() можно записать
можно записать
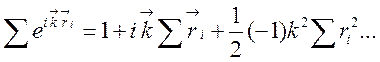 (157)
(157)
При случайном характере рассеяния
сумма всех нечетных членов разложения (157) равна нулю, а среднеквадратичное
отклонение ![]() , где
, где 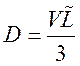 —
коэффициент диффузии. Таким образом, из (157) получим
—
коэффициент диффузии. Таким образом, из (157) получим
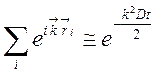 (158)
(158)
Следовательно, величина излучаемого поля, с учетом пространственной переменной, равна
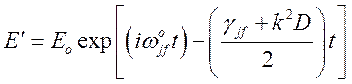 (159)
(159)
и, согласно (152, 153), имеем
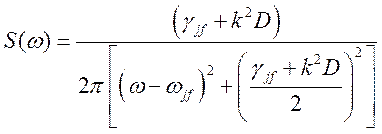 , (160)
, (160)
где ![]() —
собственная ширина линии.
—
собственная ширина линии.
Рассмотрим
смысл полученного результата. Вновь вернемся к ситуации, при которой газ при
нормальной температуре и малой плотности имеет допплеровское уширение линий с ![]() , величина которого существенно больше
естественной ширины
, величина которого существенно больше
естественной ширины ![]() . Если при увеличении
плотности газа и сохранении температуры начинает возрастать частота
столкновений, которая не меняет фазу, но изменяет скорость частицы, то должно
произойти “выключение” допплеровского уширения, а линия трансформируется в
(156) с шириной cогласно (160)
. Если при увеличении
плотности газа и сохранении температуры начинает возрастать частота
столкновений, которая не меняет фазу, но изменяет скорость частицы, то должно
произойти “выключение” допплеровского уширения, а линия трансформируется в
(156) с шириной cогласно (160) 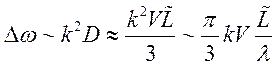 , где
, где![]() — длина свободного пробега.
Таким образом, ширина линии оказывается меньше допплеровского уширения в отношении
— длина свободного пробега.
Таким образом, ширина линии оказывается меньше допплеровского уширения в отношении
![]() .
.
При нормальных
условиях (p ~ 1 атм) 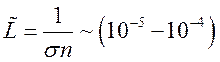 см, в
зависимости от сорта газа.
см, в
зависимости от сорта газа.
Таким образом,
для видимой области спектра (![]() ) эффект будет заметен
при давлениях
) эффект будет заметен
при давлениях ![]() . При этом столкновения не должны
влиять на время жизни атома, то есть частота тушащих столкновений, приводящих к
сбою фазы, не должна быть больше
. При этом столкновения не должны
влиять на время жизни атома, то есть частота тушащих столкновений, приводящих к
сбою фазы, не должна быть больше 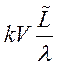 . Это означает, что необходимо
выбирать такие условия опытов (то есть сорт газа и т.п.), чтобы сбой фазы
излучения, то есть безизлучательный переход из состояния j происходил не
при каждом столкновении, а, например, только при одном из десяти.
. Это означает, что необходимо
выбирать такие условия опытов (то есть сорт газа и т.п.), чтобы сбой фазы
излучения, то есть безизлучательный переход из состояния j происходил не
при каждом столкновении, а, например, только при одном из десяти.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.