Анализ взаимодействия излучения с веществом целесообразно начать с оценок вероятностей электродинамических процессов. Точные вычисления этих вероятностей сложны и требуют использования аппарата квантовой электродинамики, чего мы делать не будем.
Основным параметром в оценках является постоянная тонкой структуры [1]
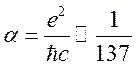 .
.
С ее помощью
устанавливается связь между тремя основными размерами: ![]() —
боровский радиус,
—
боровский радиус, ![]() - комптоновская длина и
- комптоновская длина и ![]() - классический радиус электрона.
- классический радиус электрона.
При
локализации частицы на масштабе ![]() из соотношения
неопределенности для ее энергии получим оценку
из соотношения
неопределенности для ее энергии получим оценку ![]() , т.е.
необходимо переходить к учету релятивистских эффектов.
, т.е.
необходимо переходить к учету релятивистских эффектов.
Размер водородоподобного атома с ядром заряда Z равен
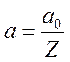 .
.
Скорость электрона в атоме
 ,
,
т.е. релятивистские эффекты необходимо учитывать при ![]() . Энергия связи
. Энергия связи
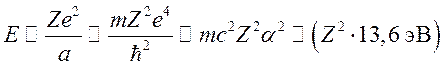
При переходе
электрона с уровня с главным квантовым числом ![]() на
на ![]()
![]() излучается фотон с
частотой
излучается фотон с
частотой
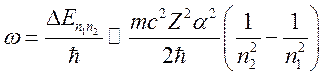
того же порядка, что и классическая частота обращения электрона на орбите
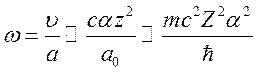 .
.
При этом длина волны излучения оказывается существенно больше размеров атома:
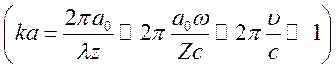 при
при 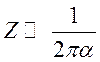 .
.
Интенсивность дипольного излучения электрона в единицу времени можно оценить по классической формуле:
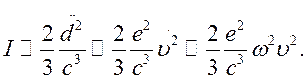
Для осциллятора
с частотой ![]() вероятность перехода в единицу времени
вероятность перехода в единицу времени
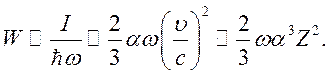 (1.1)
(1.1)
Время жизни осциллятора в возбужденном состоянии
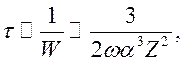
т.е. один квант излучается за ![]() периодов колебаний. Учитывая, что
периодов колебаний. Учитывая, что ![]() для
для ![]() резонансных
переходов в основное состояние, получим
резонансных
переходов в основное состояние, получим
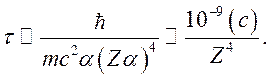
Ширина уровня
с испусканием кванта с энергией ![]() с учетом (1.1) равна
с учетом (1.1) равна
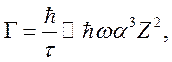
т.е. ![]()
Предельная длина светового цуга, т.е. длина когерентности,
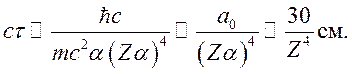
Учитывая, что как
![]() , так и
, так и ![]() зависят от Z, то можно получить связь между временем жизни
зависят от Z, то можно получить связь между временем жизни ![]() и частотой излучаемого кванта,
которую обычно наблюдают в экспериментах
и частотой излучаемого кванта,
которую обычно наблюдают в экспериментах
 (1.2)
(1.2)
при ![]() получим
получим
![]() Данная формула описывает любые, в том числе
и нерезонансные, переходы.
Данная формула описывает любые, в том числе
и нерезонансные, переходы.
Таким образом,
возбужденные состояния распадаются. Число атомов в возбужденном состоянии
описывается законом распада ![]() или
или ![]() . Вероятность излучения в единицу времени
для каждого атома, находящегося в возбужденном состоянии вплоть до времени t, равна
. Вероятность излучения в единицу времени
для каждого атома, находящегося в возбужденном состоянии вплоть до времени t, равна
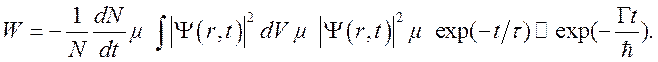
Подобная зависимость волновой функции от времени получается, если энергия уровня [2,3]
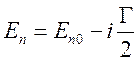 и
и 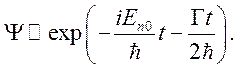
В этом случае
излучение не будет чисто гармоническим. Предполагая, что ![]() при t < 0, т.е. атом не был возбужден, и
при t < 0, т.е. атом не был возбужден, и ![]() при
при ![]() из
формул преобразований Фурье получим:
из
формул преобразований Фурье получим:
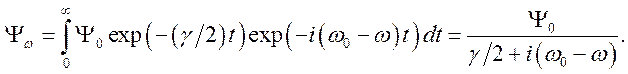
Отсюда вероятность излучения, отнесенная к единичному интервалу частот,
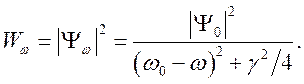
Учитывая, что
интенсивность излучения ![]() и полагая значение
и полагая значение ![]() - в центре линии, получим
- в центре линии, получим
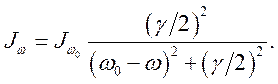 (1.3)
(1.3)
Именно такое
распределение интенсивности наблюдается при регистрации отдельных переходов
спектральными приборами. Естественной шириной линии считается отклонение
частоты от ![]() , на котором
интенсивность уменьшается в 2 раза, т.е
, на котором
интенсивность уменьшается в 2 раза, т.е ![]()
Если с уровня k возможно несколько переходов на нижележащие уровни i, то вероятности переходов ![]() складываются:
складываются:
![]() где
где ![]() - полная
вероятность,
- полная
вероятность, ![]() - время жизни k-ого
уровня. Расширение энергетических уровней приводит к расширению спектральных
линий, возникающих при переходе между ними. Так, если ширина верхнего и нижнего
уровней
- время жизни k-ого
уровня. Расширение энергетических уровней приводит к расширению спектральных
линий, возникающих при переходе между ними. Так, если ширина верхнего и нижнего
уровней ![]() и
и ![]() , то
ширина перехода
, то
ширина перехода ![]() равна
равна ![]() и
распределение спектральной интенсивности
и
распределение спектральной интенсивности
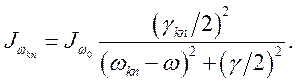 (1.4)
(1.4)
 Поскольку ширина
линии определяется суммой уширений ее начального и конечного уровней, то не
существует простого соотношения между шириной линии и ее интенсивностью.
Поскольку ширина
линии определяется суммой уширений ее начального и конечного уровней, то не
существует простого соотношения между шириной линии и ее интенсивностью.
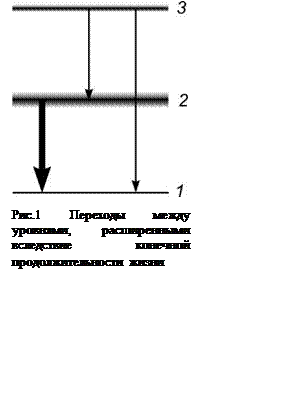
Пусть вероятность
перехода ![]() велика, а
велика, а ![]() и
и ![]() мала (рис 1). В соответствии с этим
уровень 2 – размыт, а уровень 3 – узкий. Линия 2 → 1 будет широкой и
интенсивной. Линия 3 → 2 будет еще более широкой (
мала (рис 1). В соответствии с этим
уровень 2 – размыт, а уровень 3 – узкий. Линия 2 → 1 будет широкой и
интенсивной. Линия 3 → 2 будет еще более широкой (![]() ), однако слабой, менее интенсивной и,
наконец, линия 3 → 1 будет узкой и слабой.
), однако слабой, менее интенсивной и,
наконец, линия 3 → 1 будет узкой и слабой.
Если атомы
участвуют в движении, то частота наблюдаемого света изменяется за счет эффекта
Допплера ![]() .
.
Излучение ![]() , приходящееся на интервал частот
, приходящееся на интервал частот ![]() ,
, ![]() пропорционально
числу частиц с такой скоростью
пропорционально
числу частиц с такой скоростью ![]() , что излучаемая ими
частота
, что излучаемая ими
частота ![]() приходится на данный интервал. Из
приходится на данный интервал. Из
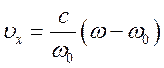
и
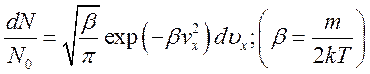 (1.5)
(1.5)
получим
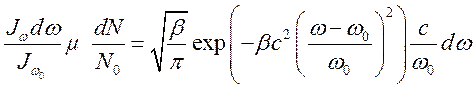 (1.6)
(1.6)
или
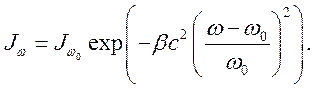
Ширина
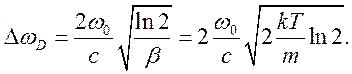
Оценки показывают, что в естественных
условиях ![]()
![]()
что в 40 раз больше собственной ширины
линии ![]()
Явление Допплера и естественное затухание – независимые друг от друга причины уширения. Поэтому реальный контур линии определяется как результат действия обоих факторов [3]:
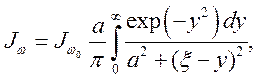 (1.7)
(1.7)
где
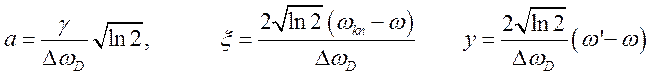
Расширение
линии, вызванное взаимодействием между атомами, рассмотрим на примере
простейшей теориии Лоренца [3]. Будем предполагать, что время ![]() между двумя столкновениями значительно
меньше времени жизни атома
между двумя столкновениями значительно
меньше времени жизни атома ![]() в возбужденном
состоянии. Учитывая, что немонохроматичность волны, опредяемая
в возбужденном
состоянии. Учитывая, что немонохроматичность волны, опредяемая ![]() , равна
, равна ![]() получим,
что набег фазы за время между двумя столкновениями обусловленный естественным
уширением:
получим,
что набег фазы за время между двумя столкновениями обусловленный естественным
уширением: ![]() , и можно считать, что в течение
, и можно считать, что в течение ![]() излучается монохороматическая волна.
Следовательно, энергия электрона
излучается монохороматическая волна.
Следовательно, энергия электрона ![]() и волновая функция
и волновая функция ![]() при
при ![]() и
и ![]() при
при ![]() и
и ![]() , где
, где ![]() и
и ![]() - моменты времени между столкновениями.
- моменты времени между столкновениями.
Предполагаем, что после столкновения электрон полностью «забывает» о своем предыдущем состоянии. Распределение по частотам определяется интегралом Фурье:
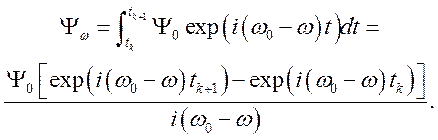 (1.8)
(1.8)
Тогда
вероятность излучения в единицу времени частоты ![]() при
времени пробега
при
времени пробега ![]() равна
равна
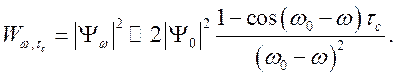 (1.9)
(1.9)
Распределение
атомов по временам пробега ![]() описывается выражением
описывается выражением
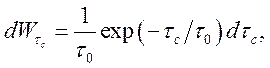
где ![]() -
среднее время свободного пробега. Тогда средняя величина вероятности излучения
равна
-
среднее время свободного пробега. Тогда средняя величина вероятности излучения
равна
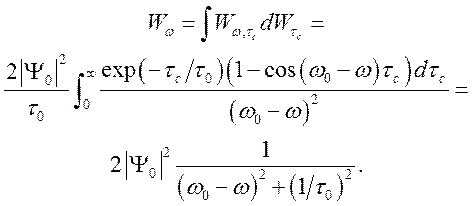 (1.10)
(1.10)
Отсюда для интенсивности излучения получим
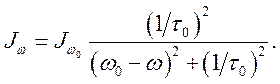 (1.11)
(1.11)
Ширина
спектральной линии ![]() Частота столкновений равна
Частота столкновений равна ![]() при нормальных условиях газа
при нормальных условиях газа ![]() Учитывая, что естественный и лоренцовский
контуры описываются одинаково, то их суммарный контур может быть представлен в
виде
Учитывая, что естественный и лоренцовский
контуры описываются одинаково, то их суммарный контур может быть представлен в
виде
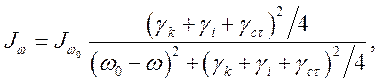 (1.12)
(1.12)
где ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.