Система с логическим управлением. Учёт времени запаздывания.
Космический аппарат первоначально вращается вокруг своей оси. Рассмотрим автоматическую систему его стабилизации при отсутствии внешних возмущений.
Структурная схема системы стабилизации и характеристики измерителей угла и угловой скорости:
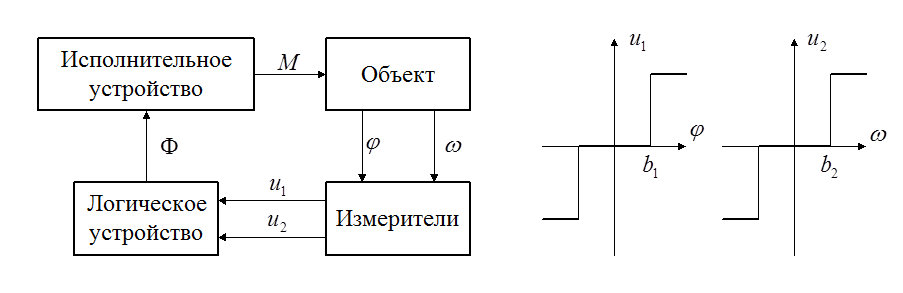
Уравнение вращения объекта:
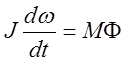 .
.
Здесь J – момент инерции, M –
вращающий момент, ![]() – логическая управляющая
функция, принимающая значения
– логическая управляющая
функция, принимающая значения ![]() (направление тяги):
(направление тяги):
Простейшая
логическая функция ![]() :
:
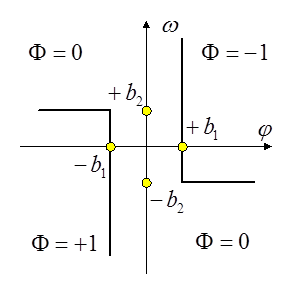
Работа системы управления без запаздывания сигналов по всей цепи.
Уравнения движения системы:
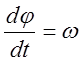 ,
, 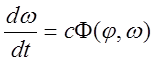 , где
, где 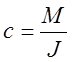 – угловое ускорение.
– угловое ускорение.
Дифференциальное уравнение фазовых траекторий:
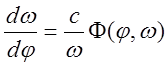 .
.
Фазовую плоскость ограничим по оси
абсцисс значениями ![]() , причём точки
, причём точки ![]() совпадают (полный оборот).
совпадают (полный оборот).
В области, где ![]() , уравнения фазовых траекторий принимают
вид
, уравнения фазовых траекторий принимают
вид ![]() , вследствие чего фазовые траектории
являются параболами с рогами налево:
, вследствие чего фазовые траектории
являются параболами с рогами налево:
![]() .
.
В области, где ![]() , фазовые траектории также являются
параболами, но с рогами направо:
, фазовые траектории также являются
параболами, но с рогами направо:
![]() .
.
В области, где ![]() , получаются прямые линии
, получаются прямые линии ![]() .
.
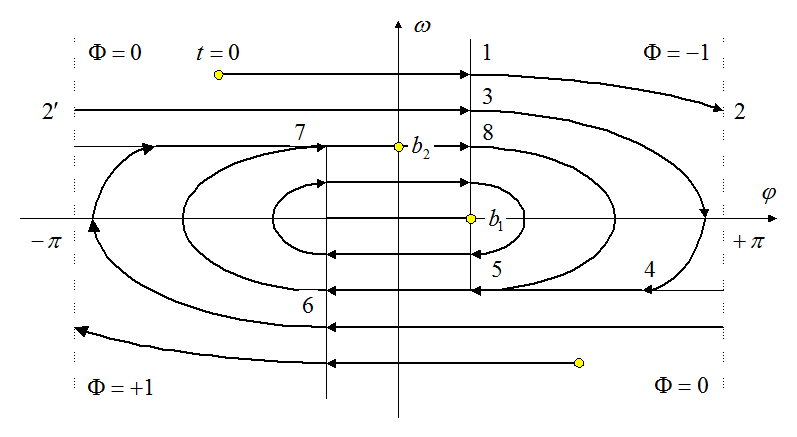
Объект входит в установившийся автоколебательный режим с амплитудой:
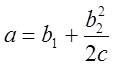 .
.
Своеобразие
предельного цикла – неасимптотическое приближение, за конечное число колебаний
(и за конечное время). Кроме того, фазовые траектории внутри предельного цикла
тоже замкнутые. Состояние равновесия, возможное только на отрезке (![]() ,
, ![]() ), не
является устойчивым. Этот отрезок аналогичен точке типа «центр».
), не
является устойчивым. Этот отрезок аналогичен точке типа «центр».
Работа системы управления при наличии запаздывания сигналов.
Пусть ![]() – время запаздывания включения сопел, а
– время запаздывания включения сопел, а ![]() – время запаздывания выключения (
– время запаздывания выключения (![]() ).
).
Поскольку к
линии включения сопел ![]() объект подходит с постоянной
скоростью, то угол включения увеличится на величину
объект подходит с постоянной
скоростью, то угол включения увеличится на величину ![]() . То
есть эффективные линии включения повернутся по ходу фазовых траекторий
вокруг точек (
. То
есть эффективные линии включения повернутся по ходу фазовых траекторий
вокруг точек (![]() ,
, ![]() ) и
займут наклонное положение.
) и
займут наклонное положение.
Поскольку к
линии выключения сопел ![]() объект подходит с постоянным
ускорением
объект подходит с постоянным
ускорением ![]() , то эффективные линии выключения окажутся смещёнными
на величину
, то эффективные линии выключения окажутся смещёнными
на величину ![]() .
.
Изменится картина фазовых траекторий и внутри предельного цикла.
Эффективная
линия переключения, согласно уравнению для фазовых траекторий ![]() , выходящих из области
, выходящих из области ![]() , пройдёт через точки:
, пройдёт через точки:
(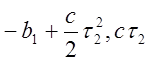 ), (
), (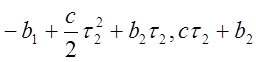 ).
).
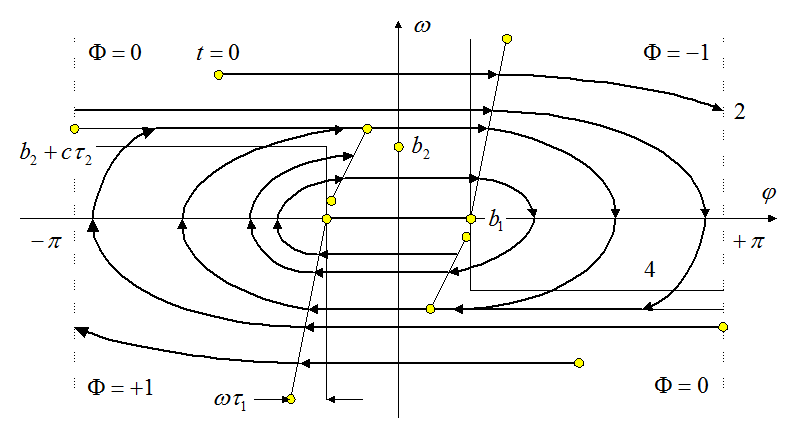
В результате внутри предельного цикла получаются расходящиеся фазовые траектории.
Таким образом исследование поведения системы высокого порядка может быть осуществлено путём исследования системы второго порядка, с учётом времени запаздывания.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.