Частотные критерии качества. Применение изодромных устройств. Комбинированное управление

Частотные критерии качества [1, с.233].

          Запас устойчивости можно определять по удалению амплитудно-фазовой характеристики разомкнутой системы от точки (). Для этой цели вводятся понятия запаса устойчивости по амплитуде и запаса устойчивости по фазе.

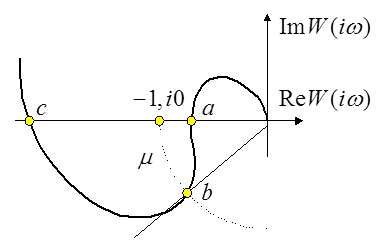
Удобнее, однако, определять запас устойчивости по показателю колебательности .

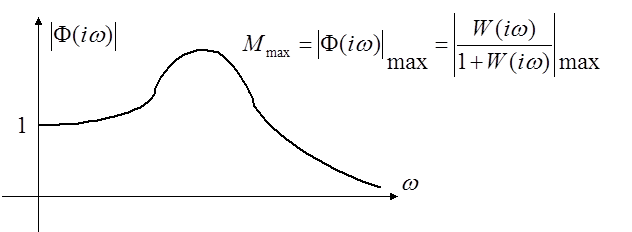
Показатель колебательности замкнутой системы можно определить по виду амплитудно-фазовой характеристике разомкнутой системы. Рассмотрим уравнение

.

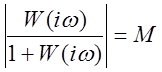Сделаем подстановки , . Тогда

.

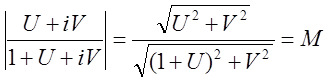Возведём в квадрат и преобразуем:

, где , .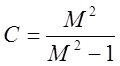

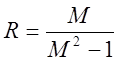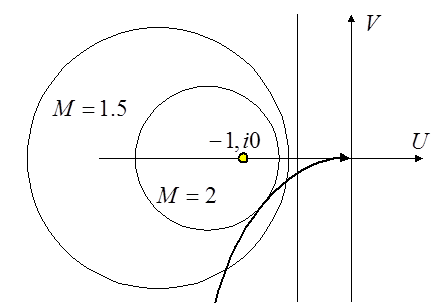
Слева – уравнение окружности с радиусом R и с центром, смещённым влево от начала координат на С. Задаваясь М от 0 до , строят семейство таких окружностей. При  окружность вырождается в прямую линию, параллельную оси ординат, проходящую через точку (). При  окружность вырождается в точку (). При  окружность вырождается в точку ().

Повышение точности систем автоматического регулирования [1, c.246].

          Общие методы:

1)      увеличение коэффициента усиления разомкнутой цепи,

2)      повышение степени астатизма,

3)      применение регулирования по производным от ошибки.

При повышении коэффициента усиления система, как правило, приближается к колебательной границе устойчивости. Следует одновременно повышать запас устойчивости, что делается с помощью различных корректирующих звеньев.

          Применение изодромных устройств.

          Можно повысить порядок астатизма без заметного ухудшения запаса устойчивости. Передаточная функция изодромного устройства:

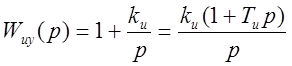, здесь .

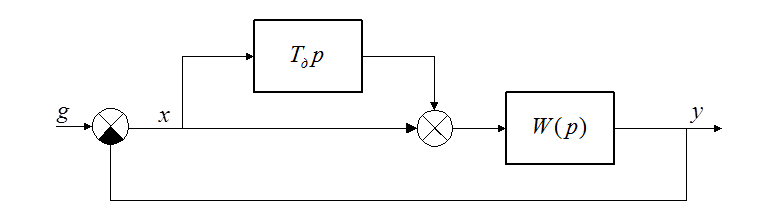
Структурная схема замкнутой системы:

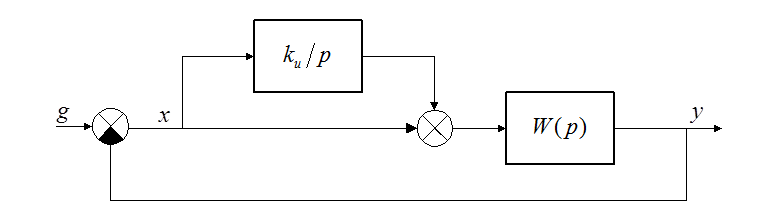
Выше были рассчитаны коэффициенты ошибок для системы, имеющей в разомкнутом состоянии передаточную функцию

.

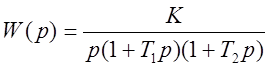Напомним процедуру получения коэффициентов ошибок.

          Передаточная функция по ошибке:

.

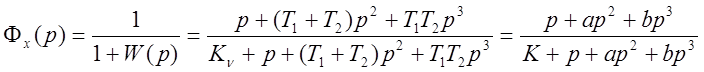Деление полинома на полином уголком:

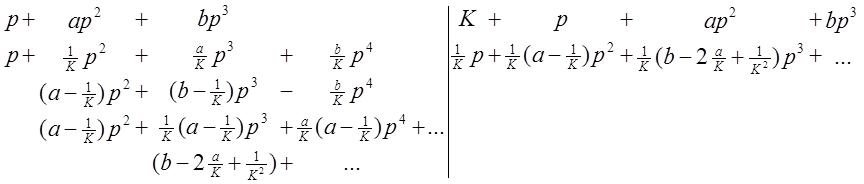
Теперь .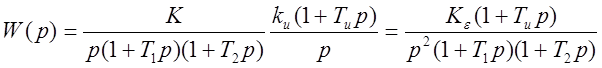

Здесь  – так называемая добротность системы по ускорению.

Коэффициенты ошибок получаются путём разложения передаточной функции замкнутой системы по ошибке . В результате:

.

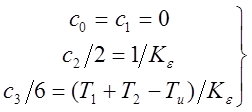Устойчивость.

Характеристическое уравнение:

.

Критерий Рауса-Гурвица:

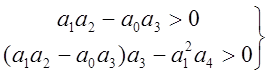
Второе неравенство более суровое:

.

Иначе:

.

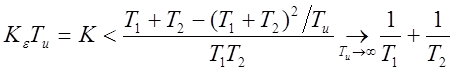Эффект изодромного устройства изображён с помощью логарифмических частотных характеристик ниже.

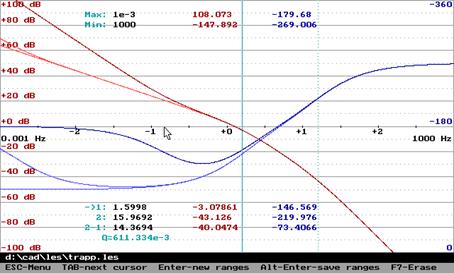
Регулирование по производным от ошибки.

          Передаточная функция дифференцирующего элемента:

.

Для той же передаточной функции разомкнутой системы, что и в примере выше, с учётом дифференцирующего звена имеем

.

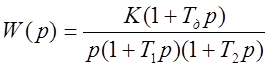Коэффициенты ошибок получаются путём разложения передаточной функции замкнутой системы по ошибке

:

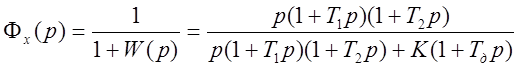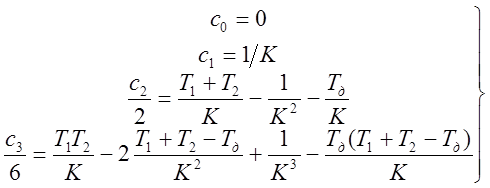
Видно, что при соответствующем выборе величины постоянной времени  можно занулить коэффициенты ошибки  или . Применяя два дифференцирующих звена, можно занулить их одновременно. Заметим, что на коэффициент  дифференцирующее звено не влияет.

          Наиболее эффективным является одновременное применение изодромных устройств и дифференцирующих звеньев.

Комбинированное управление [1, с. 254].

          Структурная схема системы с комбинированным управлением:

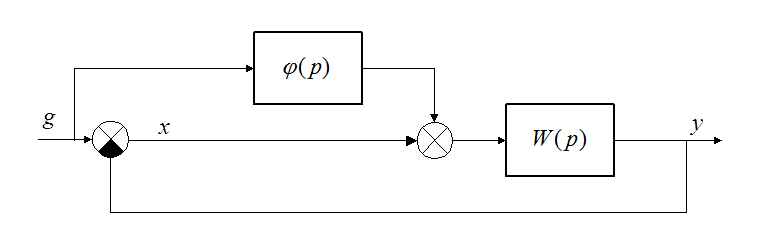
Здесь наряду с регулирование по ошибке используется регулирование по задающему воздействию. Регулируемая величина определяется выражением:

.

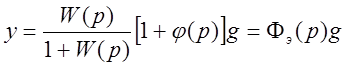Видно, что введение регулирования по задающему воздействию не меняет характеристического уравнения системы, работающей по отклонению.

Очевидно, что если , то имеет место так называемое условие полной инвариантности системы регулирования. Т.е. эквивалентная передаточная функция по ошибке

.

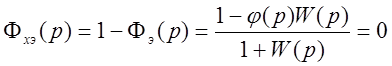На практике полная инвариантность невозможна.

Произведём разложение в ряд:

.

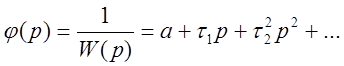Использованием конечного числа членов полученного ряда достигается частичная инвариантность. Так, введением первой производной от задающего воздействия в системе с астатизмом первого порядка можно получить равной нулю скоростную ошибку, т.е. повысить степень астатизма.

          Прежде рассмотрения некоторых примеров, рассмотрим систему, имеющую следующую структуру (сигнал регулирования по задающему воздействию подан в некоторую точку внутри канала регулирования):

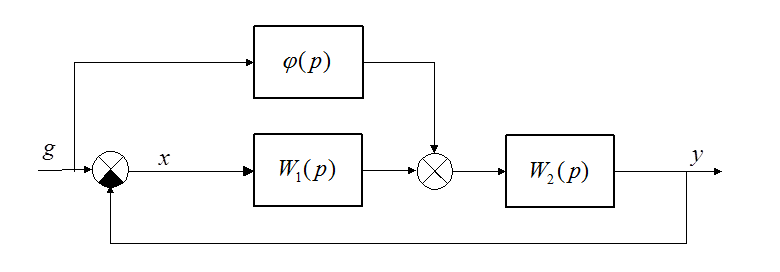
Эквивалентные передаточные функции замкнутой системы и по ошибке:

, .

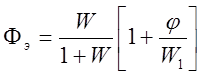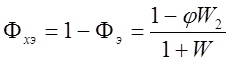Эквивалентная передаточная функция разомкнутой системы:

.

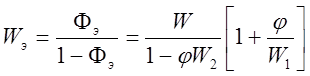Пример. Следящая система.

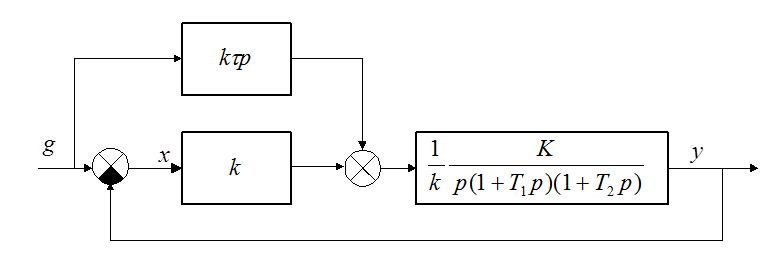
Эквивалентная передаточная функция по ошибке:

.

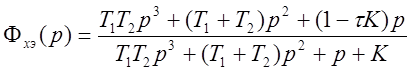Скоростная ошибка будет равна нулю, если . При этом эквивалентная передаточная функция разомкнутой системы будет соответствовать астатизму второго порядка:

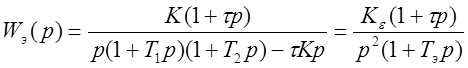, здесь , .

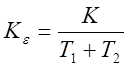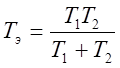Пример. Инерционная вертикаль.

          На перемещающейся горизонтально по поверхности земли платформе установлен измеритель горизонтального ускорения:

.

Здесь  – наклон платформы (ошибка вертикали), R – радиус Земли,  – угол, соответствующий пройденному пути . Двойной интеграл от этого ускорения поворачивает платформу на угол .

          Система стабилизации вертикали описывается следующей структурной схемой:

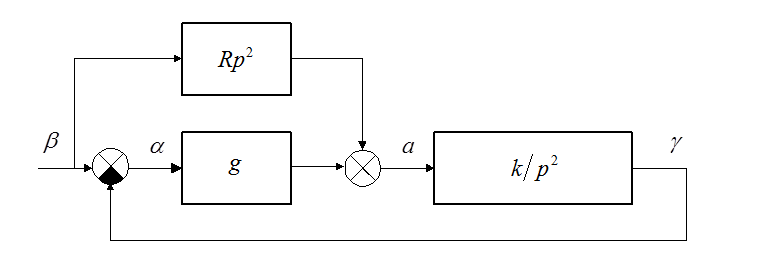
Передаточная функция по ошибке (вертикали):

.

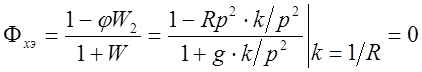Всё это справедливо, если выполнены нулевые начальные условия – отсутствует свободное начальное движение вертикали. В самом деле, характеристическое уравнение имеет вид:

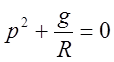, корни: .

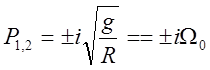Здесь  – частота незатухающих колебаний вертикали, которой соответствует период , называемый периодом Шулера.