Частотный критерий устойчивости В.М. Попова.
Критерий Попова (ударение на первом «о», так как Попов – болгарин) даёт достаточные условия абсолютной устойчивости нелинейной системы по виду частотной характеристики линейной части системы.
Пусть в системе
имеется одна однозначная нелинейность. Рассмотрим случай расположения
нелинейности в секторе [![]() ]:
]:
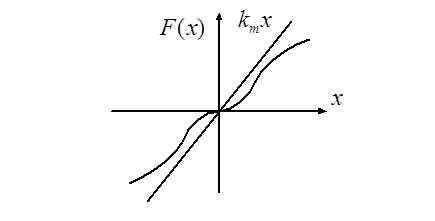
Линейная часть системы описывается уравнением:
![]() .
.
Пусть степень
полинома ![]() больше степени полинома
больше степени полинома ![]() и пусть передаточная функция линейной
части
и пусть передаточная функция линейной
части ![]() имеет полюсы с отрицательными
вещественными частями и не более двух нулевых полюсов.
имеет полюсы с отрицательными
вещественными частями и не более двух нулевых полюсов.
Теорема Попова.
Состояние
равновесия нелинейной системы будет абсолютно устойчивым, если нелинейная
характеристика находится в секторе [![]() ]
и существует такое действительное число h, что
при всех
]
и существует такое действительное число h, что
при всех ![]() выполняется неравенство
выполняется неравенство
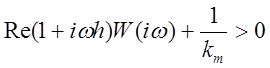 .
.
Введём модифицированную частотную характеристику линейной части:
![]() , где
, где ![]() , а
, а ![]() .
.
Выражение из формулировки теоремы Попова можно записать в виде
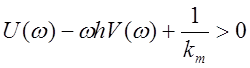 или
или 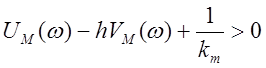 .
.
Выражение ![]() представляет собой уравнение прямой,
проходящей через точку
представляет собой уравнение прямой,
проходящей через точку ![]() на оси
на оси ![]() с
наклоном
с
наклоном ![]() . Отсюда имеем следующую формулировку
критерия Попова:
. Отсюда имеем следующую формулировку
критерия Попова:
Состояние
равновесия нелинейной системы абсолютно устойчиво, если нелинейная
характеристика находится в секторе [![]() ]
и можно провести через точку
]
и можно провести через точку ![]() прямую так, что она не
пересечёт модифицированную частотную характеристику. Слева на рисунке показан
случай устойчивой системы, а справа – неустойчивой.
прямую так, что она не
пересечёт модифицированную частотную характеристику. Слева на рисунке показан
случай устойчивой системы, а справа – неустойчивой.
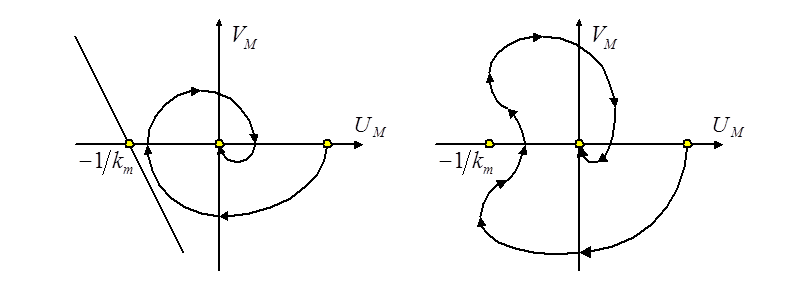
Рассмотрим случай расположения
нелинейности в секторе [![]() ].
].
Теперь неравенство в теореме Попова приобретает вид:
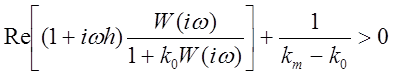 .
.
Происхождение этого соотношения поясняется эквивалентным преобразованием структурной схемы системы:
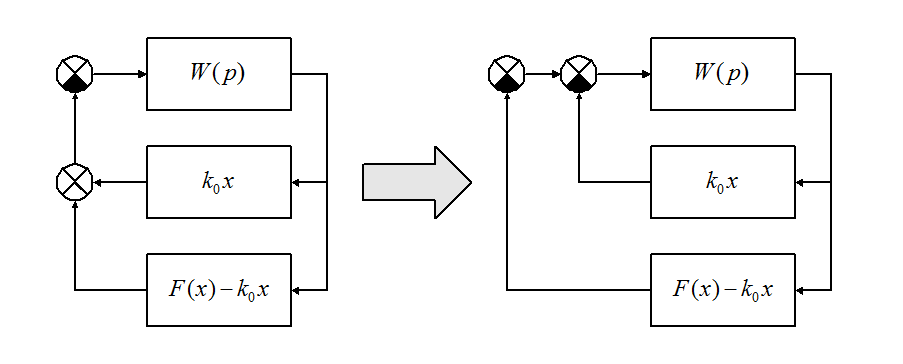
Преобразование этого выражения даёт:
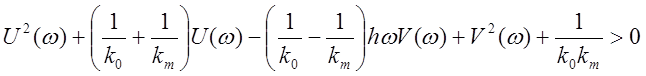 .
.
На плоскости координат модифицированной частотной характеристики уравнение
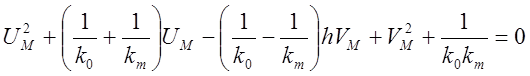
описывает параболу, проходящую
через точки ![]() и
и ![]() , и
имеющую в этих точках крутизну наклона касательных
, и
имеющую в этих точках крутизну наклона касательных ![]() и
и ![]() , соответственно.
, соответственно.
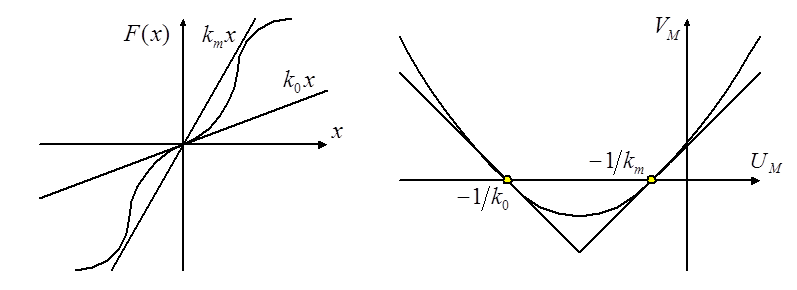
Формулировка критерия:
Состояние
равновесия нелинейной системы будет абсолютно устойчиво, если нелинейная
характеристика находится в секторе [![]() ]
и можно провести через точки
]
и можно провести через точки ![]() и
и ![]() такую параболу с вертикальной осью, чтобы
модифицированная частотная характеристика линейной части лежала вне этой
параболы.
такую параболу с вертикальной осью, чтобы
модифицированная частотная характеристика линейной части лежала вне этой
параболы.
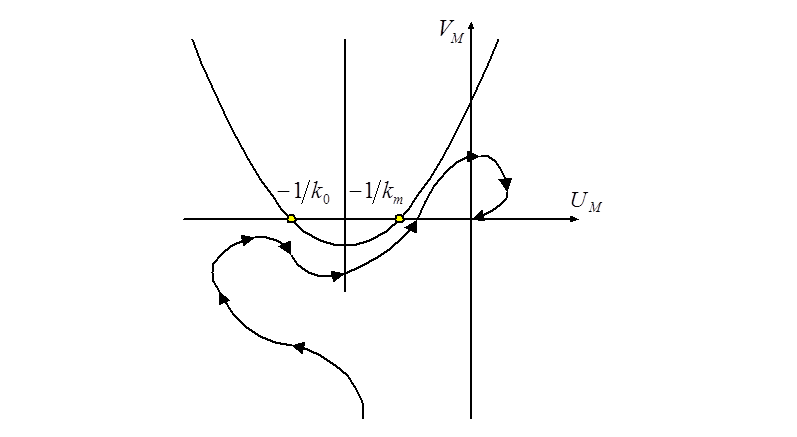
Видно, что здесь нельзя провести
прямую через точку ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.