Алгебраический способ определения симметричных колебаний и устойчивости

Алгебраический способ определения симметричных колебаний и устойчивости.

Пусть система имеет следующую передаточную функцию линейной части (обладающую свойством фильтра):

.

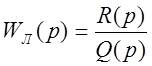Дифференциальные уравнения линейной части системы и нелинейного звена:

, , ().

Уравнение замкнутой системы:

.

Решение ищется в виде (две неизвестные величины):

.

После гармонической линеаризации

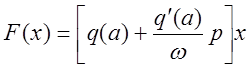
уравнение приобретает вид:

.

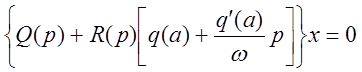Поскольку в искомом решении  и , это уравнение можно рассматривать как обыкновенное линейное уравнение с постоянными коэффициентами. Специфика заключается в том, что эти коэффициенты неизвестны.

Характеристическое уравнение:

.

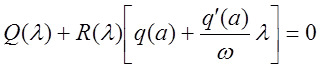Периодическое решение соответствует паре чисто мнимых корней, поэтому подставим сюда :

.

Выделим здесь вещественную и мнимую части:

.

Имеем два алгебраических уравнения, откуда находим амплитуду и частоту.

Решение упрощается в случае однозначной нелинейности. В этом случае имеем:

.

Пусть

, .

Тогда

, , или

.

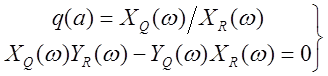Видно, что частота зависит только от вида линейной части системы и не зависит от формы однозначной нелинейности.

Приближённый способ исследования устойчивости.

Дадим малые отклонения амплитуды и частоты: , . Тогда

.

Для устойчивости периодического решения необходимо, очевидно, чтобы  и  имели одинаковые знаки. Воспользуемся символической записью:

, .

Первое решение определялось уравнением

.

Второе решение определяется уравнением

.

Разложение в ряд Тейлора в точке ():

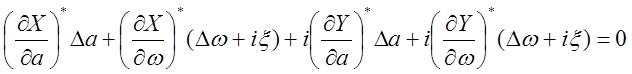
В результате исключения :

.

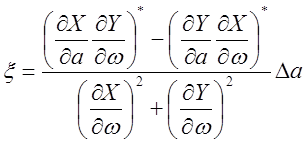Для одинаковости знаков  и  необходимо, чтобы

.

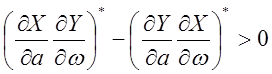Кроме этого необходимо, чтобы все остальные корни характеристического уравнения линеаризованной системы имели отрицательные вещественные части, т.е. многочлен

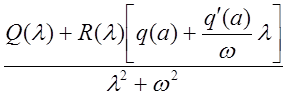
должен удовлетворять критерию Гурвица (или Михайлова).

Пример. Следящая система.

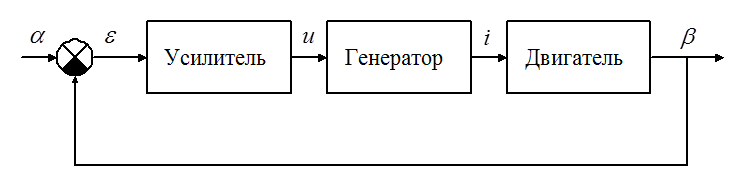
Уравнения движения:

, , , .

Уравнение линейной части при :

, .

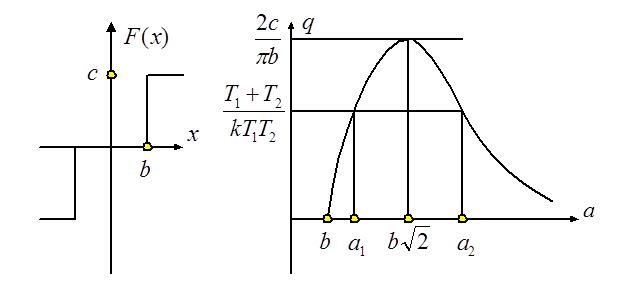
Гармонически линеаризованное уравнение замкнутой системы:

.

Здесь коэффициент гармонической линеаризации

.

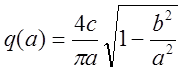Характеристическое уравнение:

.

После подстановки  имеем два уравнения:

.

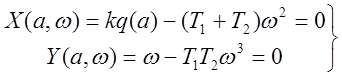Отсюда

, .

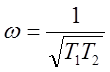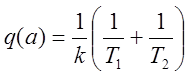Уравнение

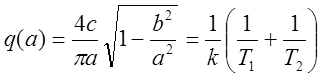
имеет два решения:  и  (см. рисунок выше). Причём в этих точках, соответственно,  и . Для определения устойчивости найдём знак выражения

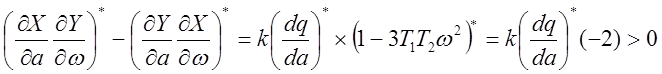 при .

Таким образом, в точке  решение неустойчиво, а в точке  – устойчиво.

На рисунке ниже изображены амплитуды автоколебаний и неустойчивого периодического решения в зависимости от коэффициента усиления линейной части системы. Граничное значение коэффициента усиления

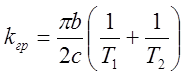
соответствует точке максимума кривой на рисунке выше.

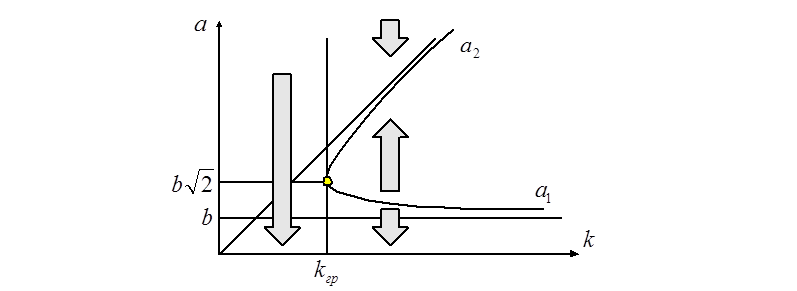
Имеется область устойчивого равновесного состояния () и область жёсткого возбуждения автоколебаний (), где требуется заброс начального состояния за линию .