Связанно-связанные переходы. Спектральные линии

Лекция № 17

Связанно-связанные переходы. Спектральные линии.

С точки зрения классической электродинамики возбужденный атом представляет собой осциллятор, излучающий в течение времени  от момента возбуждения до затухания. С точки зрения квантовой механики атом возбуждается мгновенно, затем живет в возбужденном состоянии некоторое время  и затем мгновенно испускает квант .

В рамках классического подхода излучающий атом будем представлять как систему, состоящую из положительного заряда большой массы, которой будем считать неподвижным и отрицательного заряда (по абсолютной величине равного положительному), совершающего колебания относительно неподвижного заряда. Такая система является диполем, с дипольным моментом . Для того, чтобы заряд излучал, он должен двигаться с ускорением, тогда полный поток излучаемой энергии (см. (15.8)) есть:

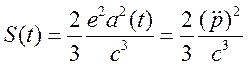                                                                              (17.1)

Пусть дипольный момент со временем меняется по гармоническому закону , тогда из (17.1) имеем

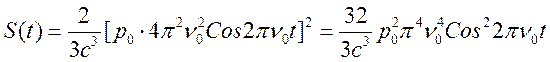                                   (17.2)

Интерес представляет не сам поток , а его среднее за период значение 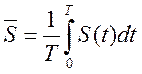 ( - период колебаний). Усредняя (17.2) получим:

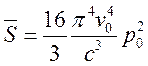                                                                                             (17.3).

Поскольку осциллятор излучает, то запас энергии его убывает и колебания затухают. Найдем закон убывания энергии. Будем, как и ранее предполагать, что за период потери энергии малы по сравнению с энергией осциллятора (что соответствует экспериментальным результатам) и колебания будем считать практически гармоническими. В этом случае для потока будет справедлива формула (17.3) и убыль энергии осциллятора за время  есть:

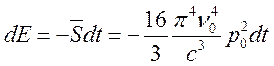                                                                           (17.4).

Разделим обе части (17.4) на полную энергию осциллятора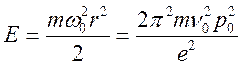

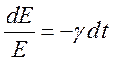                                                                                                 (17.5)

где 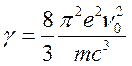 - постоянная затухания. Из (17.5) следует 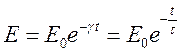,  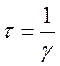   время затухания. Оценим для самой сильной линии аргона. , соответствующей переходу в основное состояние

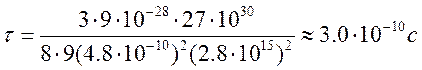
В то же время период колебаний 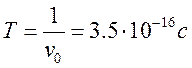, т.е.  и наше предположение справедливо.

Для получения спектрального состава излучения его необходимо разложить в интеграл Фурье. Для случая слабого затухания зависимость дипольного момента от времени есть:

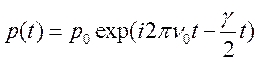                                                                            (17.6)

Амплитуда спектрального разложения  находится из (17.6) преобразованием Фурье:

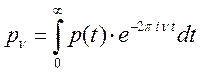
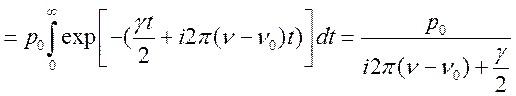                     (17.7)

Подставим спектральную амплитуду  в выражение для среднего спектрального потока 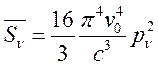  и получим частотную зависимость интенсивности излучения в спектральной линий:

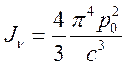
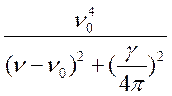                                                                       (17.8)

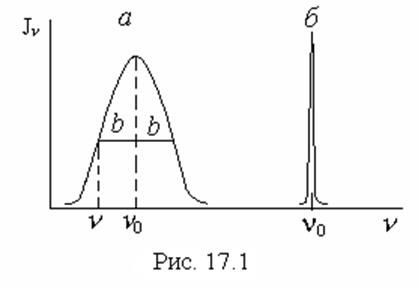На рис. 17.1 а схематично представлен контур линии излучения определяе-мый выражением (17.8). Ширину спектральной линии принято характеризовать величиной , на которой интен-сивность падает в 2 раза по сравнению с максимальной. В реальном масштабе частот, поскольку  спектральная линия представляет собой резко сингулярную линию (рис. 17.1б). Контур поглощения определяется из закона Кирхгофа  при этом, частотная зависимость остается той же, что и для линии излучения, т.к. функция Планка и поправка на вынужденное испускание практически не меняются на ширине спектральной линии.

Экспериментальные результаты качественно подтверждают частотную зависимость (17.8), однако количественный результат значительно отличается. Введение поправочного коэффициента не всегда удается выполнить даже в расчетах методами квантовой механики. Поэтому частотное распределение интенсивности излучения в спектральной линии принято описывать с помощью нормированной на единицу формы линии : .

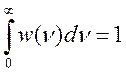Для линии (17.8) форма  имеет вид (дисперсионный контур):

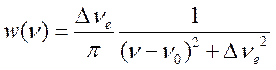                                                                          (17.9),

где  полуширина, связанная с радиационным затуханием и называется естественной полушириной.

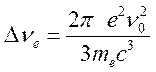                                                                                            (17.10).

Оценим ее для самой сильной резонансной линии аргона

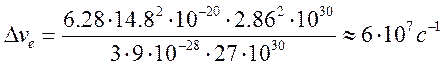
Квантовомеханическое рассмотрение изолированной спектральной линии также приводит к дисперсному контуру (17.9). Ширина линии в данном случае связана с размытием (уширением) энергии уровней перехода в силу принципа неопределенности:  из-за конечного времени жизни возбужденных состояний. Размытие уровней приводит к уширению линий на частоту  т.е. порядка «затухания»  как и в классической механике.

Коэффициент поглощения в спектральной линии имеет вид

,                                                                                              (17.11)

где 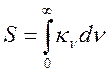 - интегральное поглощение спектральной линии, рассчитываемое через силу осциллятора  перехода , которая связана с вероятностью перехода и определяется обычно из эксперимента или квантовомеханических расчетов,

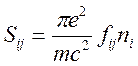                                                                                              (17.12),

где  - концентрация атомов на поглощаемом уровне.