Связанно-связанные переходы. Спектральные линии, страница 2

Изложенная выше теория уширения спектральных линий справедлива лишь для изолированных атомов. В реальных условиях атомы и ионы в газе и плазме испытывают взаимодействие с окружающими частицами, что приводит к уширению линий, гораздо большему, чем естественное и в ряде случаев к сдвигу центров линий. Кроме естественного, линии всегда уширины вследствие эффекта Доплера. Если атом вдоль линии наблюдения имеет компоненту скорости теплового движения , то квант энергии, частоты  испущенный в этом направлении будет восприниматься как квант

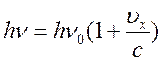                                                                                          (17.13)

При наличии ЛТР, используя Максвелловскую функцию распределения по скоростям

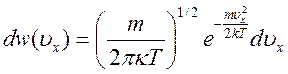                                                                                 (17.14),

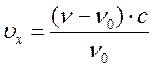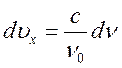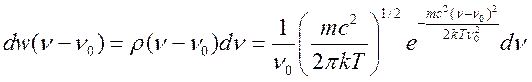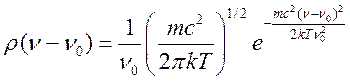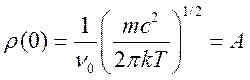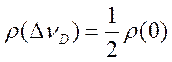получим форму доплеровского контура. Из (17.13) ;  и подставляя в (17.14) получим , где плотность функции распределения . В центре линии . По определению, на полуширине линии  плотность есть  откуда  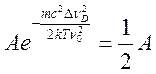и для доплеровской полуширины получаем

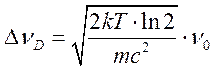                                                                                                                            (17.15).

В отличие от естественной полуширины, которая не зависит от температуры,  возрастает с температурой как . Оценим  для той же линии аргона при К.

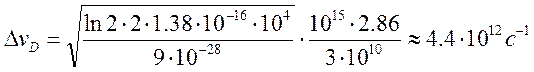
При наличии заряженных частиц (т.е. в плазме) возникает отличное от нуля локальное электрическое поле, в то время как плазма в целом квазинейтральна. Взаимодействие оптического электрона с этим полем приводит к штарковскому расщеплению энергетических уровней на систему подуровней, уширению линий и сдвигу центров линий, причем сдвиг относительно центра может быть как положительный , так и отрицательный . Для разных газов имеет место линейный или квадратичный Штарк-эффект. Так линии водорода уширяются за счет линейного Штарк-эффекта, а аргона – квадратичного. Подробные данные по штарковскому уширению линий можно найти в работе Грим Г. Уширение спектральных линий в плазме. / М.: Мир, 1978

.

В широком интервале значений электронных плотностей и температур штарковская полуширина атомных линий (в ) приближенно выражается следующей формулой

,                     (17.16)

а сдвиг линий (в )

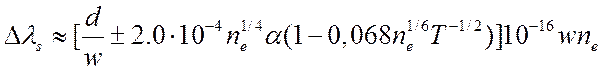                            (17.17).

Таблицы параметров составлены Гримом и приведены в [7].

Особенности в уширении имеют линии, у которых нижнее состояние является основным. Холодный газ при облучении его излучением с частотой, соответствующей таким переходам, поглощает излучение и, в свою очередь начинает излучать на тех же частотах. Это явление, открытое Вудом, было названо резонансной флоуресценцией, а соответствующие линии – резонансными, именно таковой является рассматриваемая нами в качестве примера линия аргона.

Такие линии уширяются значительно сильнее и это связано с тем, что при столкновении двух одинаковых атомов, один из которых возбужден, возможна резонансная передача энергии возбуждения, причем эффективные сечения таких столкновений могут значительно (на несколько порядков) превосходить газокинетические сечения. Связанное с этим резонансное уширение есть:

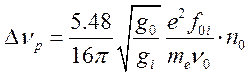                                                                              (17.18),

где  - статистический вес основного состояния,  - статистический вес уровня перехода,  - концентрация атомов в основном состоянии,  - сила осциллятора перехода .

Оценим  для линии аргона  = 1,  = 3,  = 0.254, ,  см ^{– 3}

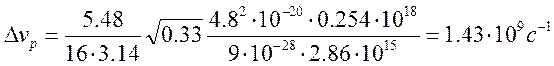
Поскольку естественное и допплеровское уширение присутствует всегда, а к ним добавляются также уширения из-за взаимодействия с окружающими частицами, то результирующая форма спектральной линии должна вычисляться с помощью процедуры свертки. В общем случае эта процедура определяется следующим образом. Если имеются две статистически независимые величины  и , описываемых функциями распределения  и , функция распределения , описывающая поведение величины , есть

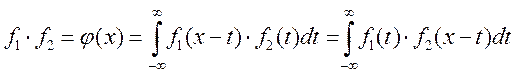
Свертка двух дисперсионных контуров (типа (17.8)) есть снова дисперсионный контур с полушириной . Свертка дисперсионного и допплеровского контуров известна под именем профиля Фойгта:

;   ; .

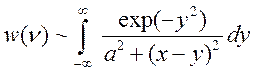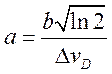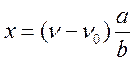Постоянная пропорциональности определяется из условия нормировки. Крылья профиля Фойгта всегда дисперсионные. При действии нескольких механизмов уширения процедура свертки должна применяться последовательно.

Окончательно, согласно (17.11) коэффициент поглощения в линии будет иметь вид

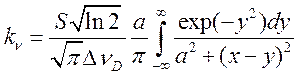                                                                      (17.19),

где:  - доплеровская полуширина; ,  - центр линии,  - штарковский сдвиг линии,  - ударный параметр, ,  - штарковская полуширина, .

 С учетом вынужденного переизлучения коэффициент поглощения в линии запишется

                                                                             (17.20).

В работе (Матвеев В.С. Приближенные представления коэффициента поглощения и эквивалентных ширин с фойгтовским контуром.// Журнал прикл. спектроскопии. 1972,Т.XVI, вып. 2, с.228-233)  дано приближенное выражение коэффициента поглощения, определяемого формулой (17.19)

;

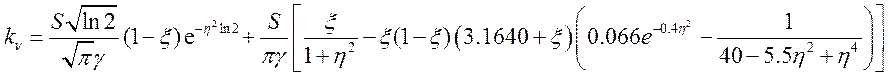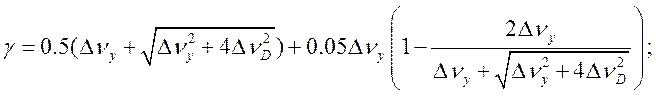
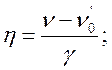
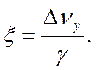 (17.21).