
Потери энергии частицей на возбуждение и ионизацию
(Зелевинский, с.262)
![]() Постановка задачи
Постановка задачи
Имеется среда, с плотностью N невзаимодействующих атомов (газ).
Все атомы находятся в основном состоянии (обозначенном 1)
Взаимодействие частицы с отдельным атомом определяется сечением неупругого рассеяния (лекция 13).
Путь, проходимый частицей в среде - х ,
Т – кинетическая энергия частицы.
![]()
![]() Общая
формула для потери энергии на единицу длины
Общая
формула для потери энергии на единицу длины
![]() Число столкновений частицы на длине пути dx с
переходом атома 1® n
Число столкновений частицы на длине пути dx с
переходом атома 1® n
![]()
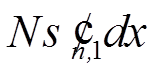 ,
,
где
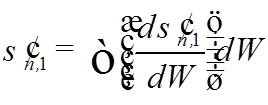 .
.
(Скорость частицы «включена» в сечение !).
![]() Энергия, теряемая частицей в каждом акте рассеяния
Энергия, теряемая частицей в каждом акте рассеяния
с возбуждением атома на n-ый уровень, равна
![]()
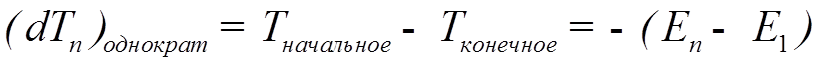 .
.
![]()
![]()
![]() Умножив
на , получим потери
энергии частицей на длине dx в канале,
соответствующем переходу атомов 1® n:
Умножив
на , получим потери
энергии частицей на длине dx в канале,
соответствующем переходу атомов 1® n:
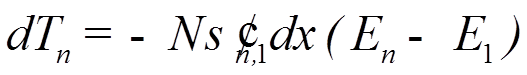
![]() Просуммировав по всем состояниям (каналам рассеяния),
получим
Просуммировав по всем состояниям (каналам рассеяния),
получим
полную потерю энергии частицей на единице
длины
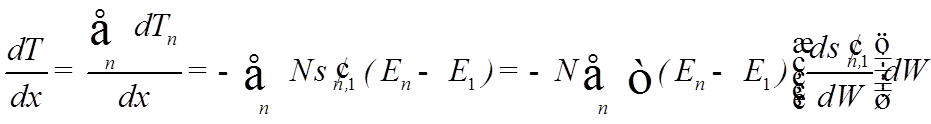
![]() Переходя от интегрирования по
Переходя от интегрирования по ![]() к
интегрированию по разностному вектору
к
интегрированию по разностному вектору ![]() (
(![]() ), (как это сделано в лекции 13), получим формулу для потерь энергии на единицу длины
), (как это сделано в лекции 13), получим формулу для потерь энергии на единицу длины
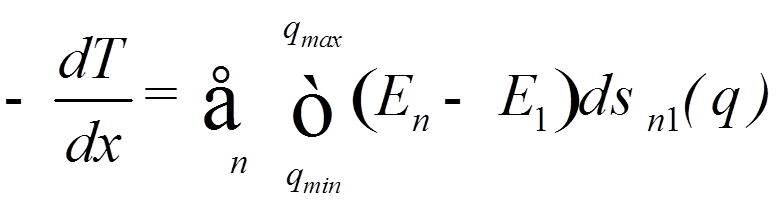 (*)
(*)
![]()
![]() Сечение
Сечение
![]()
Сечение неупругого столкновения выразим формулой из лекции 13, (Л.Л.III, §148)
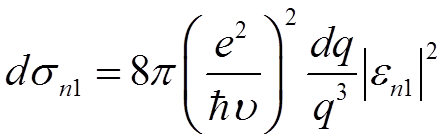 , (* *)
, (* *)
где ![]() – матричный элемент от
фурье-компонент плотности электронов в атоме (Ландау,706), равный
– матричный элемент от
фурье-компонент плотности электронов в атоме (Ландау,706), равный
.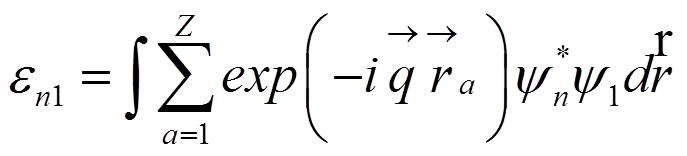 .
.
Здесь суммирование проводится
по всем электронам в атоме; 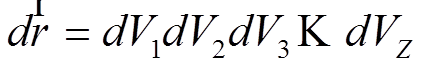 - элемент
конфигурационного пространства электронов атома;
- элемент
конфигурационного пространства электронов атома;
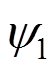 и
и ![]() - начальная и конечная
волновые функции электрона.
- начальная и конечная
волновые функции электрона.
![]() Замечание
Замечание
Дискретные и непрерывные конечные состояния отличаются нормировкой соответствующей волновой функцией
![]()
![]() Вычисление
Вычисление
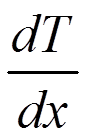
![]() Подставив (* *) в (*) можно, в принципе, вычислить
Подставив (* *) в (*) можно, в принципе, вычислить ![]() -
потерю энергии частицей на единице длины. Однако вычисление суммы в (*) сильно осложняется тем, что в силу законов сохранения пределы
интегрирования
-
потерю энергии частицей на единице длины. Однако вычисление суммы в (*) сильно осложняется тем, что в силу законов сохранения пределы
интегрирования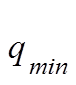 и
и 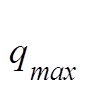 сами зависят от конечного состояния n.
сами зависят от конечного состояния n.
![]()
Теорема
суммирования (Ландау, с.715)
аналогичная более известному правилу
суммдля сил осциллятора,
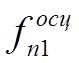 ,
существенно упрощает задачу нахождения∑ в (*).
,
существенно упрощает задачу нахождения∑ в (*).
![]()
Отметим ключевые моменты теоремы суммирования и правила сумм.
![]() Сила
осциллятора
Сила
осциллятора 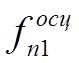
![]() По определению
По определению 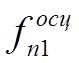 есть
отношение интенсивности спектральной линии спонтанного
излучения атома к интенсивности излучения классического диполя (осциллятора) на
собственной частоте, равной частоте перехода
есть
отношение интенсивности спектральной линии спонтанного
излучения атома к интенсивности излучения классического диполя (осциллятора) на
собственной частоте, равной частоте перехода
ωосцил= ωn1= (En-E1)/ћ.
Энергия классического осциллятора с зарядом е и массой me из-за излучения в окружающее пространство затухает по закону
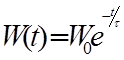
с характерным временем
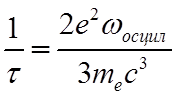
![]() Время затухания спонтанного излучения связано с вероятностью излучения Acn
соотношением
Время затухания спонтанного излучения связано с вероятностью излучения Acn
соотношением
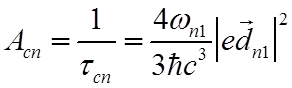
откуда
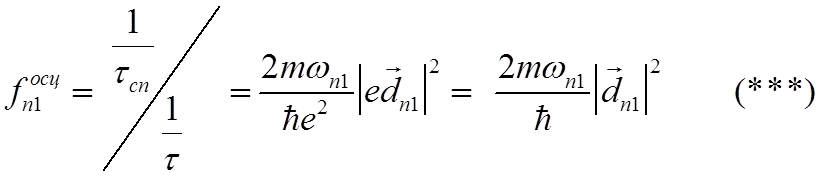
![]() Правило сумм для
Правило сумм для 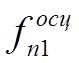 (дипольное
правило Томаса-Райхе-Куна)
(дипольное
правило Томаса-Райхе-Куна)
Безразмерная
величина 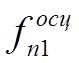 обладает удивительным свойством (правило сумм):
обладает удивительным свойством (правило сумм):
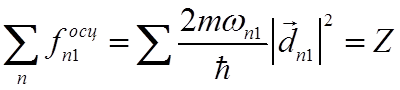
где Z – число электронов в атоме.
Доказательство правила сумм для осцилляторов см. в Лоудон, с.122 и далее; Собельман, с.403; Ландау, с.715; Давыдов, 468, Зелевинский, 135.
![]() Теорема
суммирования
Теорема
суммирования
![]() Аналогичную теорему
суммирования (Ландау, с.715) (или
правило сумм для
флуктуаций плотности,
(Зелевинский, с.136)) можно доказать для флуктуаций плотности вероятности. Для
перехода 1®n она
определяется соотношением (Зелевинский):
Аналогичную теорему
суммирования (Ландау, с.715) (или
правило сумм для
флуктуаций плотности,
(Зелевинский, с.136)) можно доказать для флуктуаций плотности вероятности. Для
перехода 1®n она
определяется соотношением (Зелевинский):
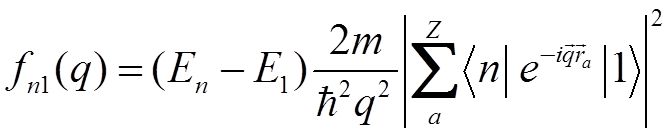 ,
, 
сумма интегралов в котором есть матричные элементы от пространственной по q фурье-компоненты плотности вероятности (заряда) в атоме.
![]() Видно, что
Видно, что  существенно отличается
от формулы для силы осциллятора
существенно отличается
от формулы для силы осциллятора ![]()
![]() .
.
![]() Можно показать, что сумма по всем состояниям от
Можно показать, что сумма по всем состояниям от  также как и для сумм для сил осцилляторов
равна Z – числу электронов в атоме:
также как и для сумм для сил осцилляторов
равна Z – числу электронов в атоме:
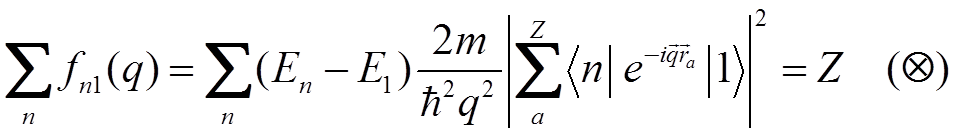
Соотношение (Ä) известно как теорема суммирования. С ее помощью легко вычисляются удельная потеря энергии частицы по формуле (*).
![]()
![]() С учетом
С учетом  выражение (*) можно
представить в виде
выражение (*) можно
представить в виде
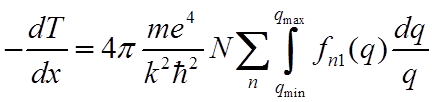
Знак интеграла нельзя вынести из под знака суммы, так как qmin = (En-E1)/ћV.
![]()
![]() Разобьем область интегрирования на два участка от qmin до q0 ≈
1/а0 и от q0 до qmax .
Разобьем область интегрирования на два участка от qmin до q0 ≈
1/а0 и от q0 до qmax .
В первой области для fn1 можно воспользоваться дипольным приближением (**) – нет зависимости от q !
![]()
Следовательно при qa0 < 1 имеем
![]()
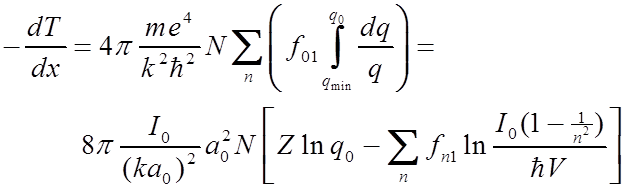 .
.
![]()
![]() В другом предельном случае qa0 > 1 получим
В другом предельном случае qa0 > 1 получим
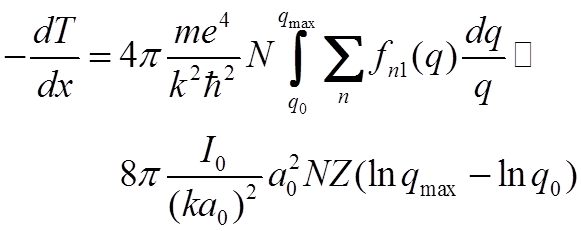
![]() Сложив оба выражения, получим
Сложив оба выражения, получим
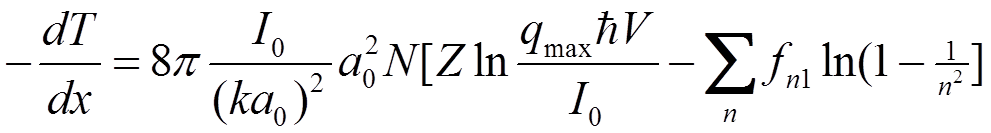
![]() Введем некоторую среднюю энергию возбуждения I1, определяемую
соотношением
Введем некоторую среднюю энергию возбуждения I1, определяемую
соотношением
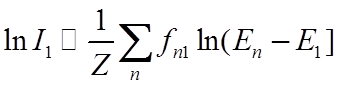
тогда
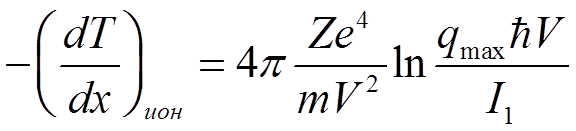 (@)
(@)
![]()
это ионизационные потери, куда входит всего одна характерная для атома постоянная I1. Для водорода она равна I1≈ 0.55(me4/ћ2) = 14.9 эВ.
Таким образом, ионизационные потери определены в зависимости от максимального импульса, который можно передать электрону атома при столкновении.
![]()
распространении легких частиц.
![]() Торможение
электрона
Торможение
электрона
![]()
При столкновении с
большой передачей импульса оба электрона (падающий и атомный)
могут приобрести сравнимые по величине скорости: ![]() нужно
учитывать обменные эффекты (частицы становятся тождественными !).
нужно
учитывать обменные эффекты (частицы становятся тождественными !).
![]()
Для быстрых электронов сечение рассеяния на Z электронах атома было определено нами ранее (лекция 13). Используя его можно показать:
![]() При передаваемой энергии, меньшей некоторого значения
При передаваемой энергии, меньшей некоторого значения ![]() , потери можно представить в виде:
, потери можно представить в виде:
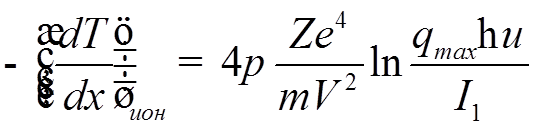 (&)- ионизационные потери.
(&)- ионизационные потери.
![]() Припередаче энергии от
Припередаче энергии от ![]() до
до
![]() , воспользовавшись ранее выведенным выражением
для сечения, получим
, воспользовавшись ранее выведенным выражением
для сечения, получим
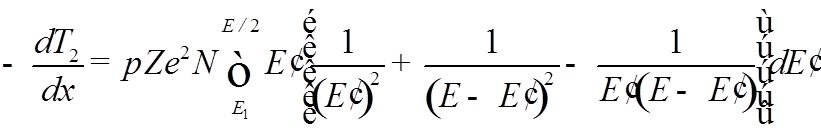 . (&&)
. (&&)
![]() Величина
Величина
![]() связана с
связана с ![]() соотношением.
соотношением.
![]() . Тогда складывая (&) с (&&) для
потерь электрона получим
. Тогда складывая (&) с (&&) для
потерь электрона получим
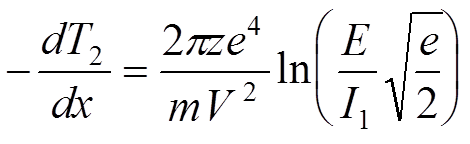 .
.
![]()
![]() Торможение
позитрона
Торможение
позитрона
![]() При рассеянии позитрона на атоме обменные
эффекты не работают и
При рассеянии позитрона на атоме обменные
эффекты не работают и ![]() можно найти из условия
можно найти из условия ![]() , т.е.
, т.е. ![]() .
Тогда
.
Тогда
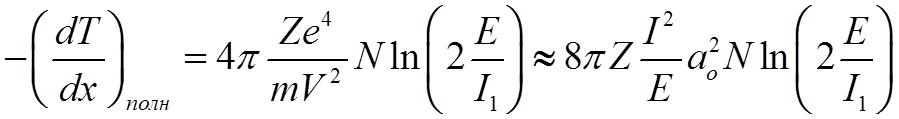 .
.
распространении тяжелых частиц.
![]() Потери
энергии частицы на ионизацию
Потери
энергии частицы на ионизацию
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.