Распространение быстрых заряженных частиц через вещество, страница 3

В отличие от ионизационных потерь, обусловленных рассеянием на электронах, радиационные потери определяются столкновением с ядром , т.к.

.

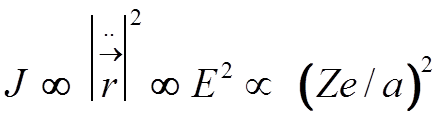Следовательно, радиационное рассеяние на ядре , тогда как рассеяние на электронах  .

 

Радиационные потери определяются соотношением

,       

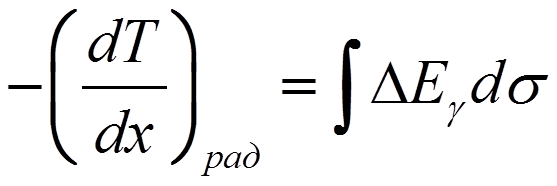где 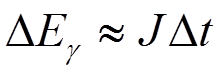, 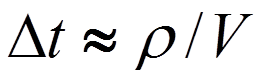 и     .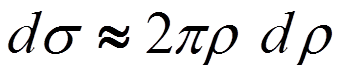

Учитывая, что   , получим

.

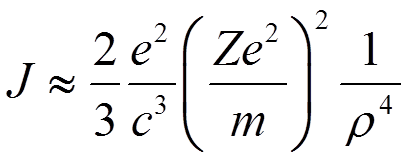
Интегрируя, окончательно получим

.

 

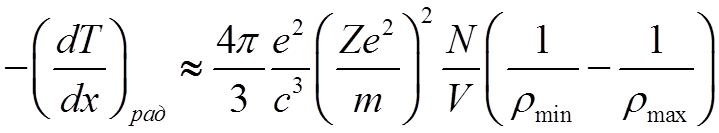Учитывая, что  и величина  должна определяться квантовыми эффектами, получим

,          (*)

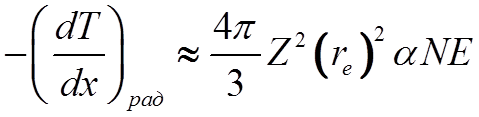где - классический радиус электрона и .

 

Для суперрелятивистской частицы кинетическая энергия Т  равна полной Е  , тогда интегрируя (*), получим

,

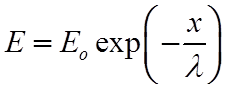где

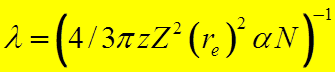- радиационная длина.

В частности, в воздухе  300 м , а в свинце  ~ 0.5 см.

 

Сравнение ионизационных и радиационных потерь

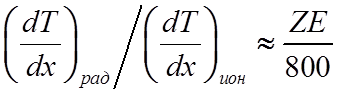 МэВ.

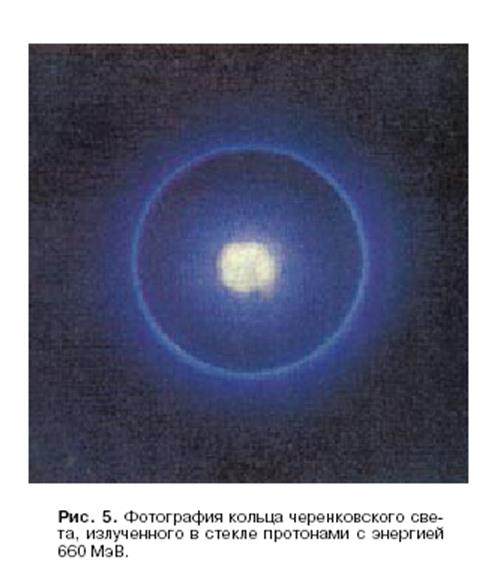
Излучение Вавилова - Черенкова

Рассмотрим заряженную частицу, двигающуюся равномерно и прямолинейно, которая теряет свою энергию на излучение.

 .           (*)

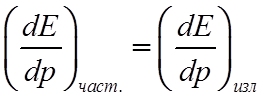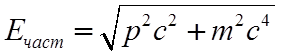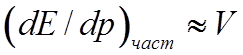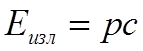Известно, что для вакуума выполнение этого равенства невозможно. Действительно, при   имеем   .     В то же время для излучения  и .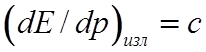

Таким образом, законы сохранения энергии и импульса запрещают заряженной частице, двигающейся равномерно и прямолинейно, отдавать свою энергию в виде излучения фотонов.

 

Однако, этот запрет снимается при движении частицы в среде с показателем  преломления n >1. В этом случае скорость фотонов

.

В случае   условие (*) выполняется для такого направления  , вдоль которого . Следовательно, излучение должно распространяться под углом

 , 

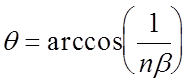где  =V/c .

 

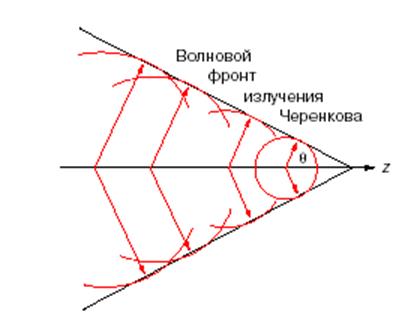
Физический механизм - когерентное излучениедиполей, возникающих в результате поляризации среды двигающейся в ней заряженной частицей.

Если частица движется медленно, возникающая поляризация распределена симметрично и результирующее поле всех диполей равно нулю.

          При движении со скоростью V>c’ наблюдается эффект запаздывания поляризации среды, в результате чего диполи имеют преимущественную ориентацию.

 

Интенсивность черенковкого излучения

Число фотонов N(ω) в интервале частот от  до  , испускаемых при прохождении единицы длины частицей с зарядом  Ze  , двигающейся со скоростью  в среде с показателем преломления n , равно

 .

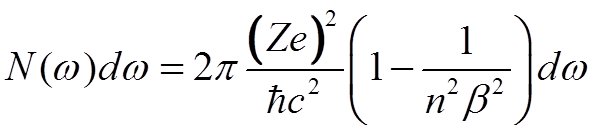Видно, что спектр одинаков для частиц с равными Z и   и различной массой.

 

Энергия излучения сконцентрирована в области высоких частот (сине-фиолетовый цвет излучения)

 .

 

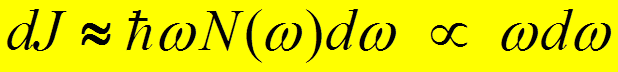Измерение скорости частицы.

Для частицы, прошедшей через тонкий слой вещества, излучение распространяется по образующей конуса с углом раствора , ось которого совпадает  с направлением движения частицы.

          Пример: для воды n = 1.33 и минимальная скорость, при которой угол излучения , равна , что соответствует кинетической энергии   МэВ.