При прохождении через вещество частицы взаимодействуют с атомами, теряя при этом свою энергию [1, 2, 11]. Для частицы, проходящей через среду, содержащую N атомов в 1 см3, потери энергии на единицу пути dT/dx равны
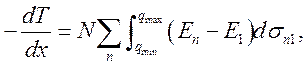 (10.1)
(10.1)
где Т — кинетическая и Е — полная энергии частиц. Суммирование в данном выражении проводится как по дискретному, так и по непрерывному спектру состояний электрона.
В качестве сечения неупругого столкновения можно взять (см. п. 7.2):
 (10.2)
(10.2)
где
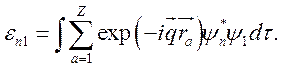 (10.3)
(10.3)
Здесь
суммирование проводится по всем электронам в атоме и ![]() и
и
![]() — начальная и конечная волновые функции
электронов.
— начальная и конечная волновые функции
электронов.
Введем понятие силы осциллятора:
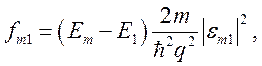 (10.4)
(10.4)
обладающей удивительным свойством [5, 6]
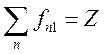 (10.5)
(10.5)
В дипольном приближении для одного электрона в атоме (10.4) можно записать в виде
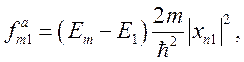 (10.6)
(10.6)
а (10.5) в этом случае оказывается равно
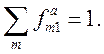
Сила осциллятора ![]() отдельного
перехода для заданного электрона характеризует относительную роль этого
перехода в полной вероятности возбуждения электрона.
отдельного
перехода для заданного электрона характеризует относительную роль этого
перехода в полной вероятности возбуждения электрона.
С учетом (10.4) и (10.2) выражение для потерь энергии можно представить в виде
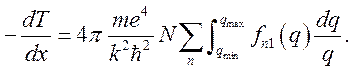 (10.7)
(10.7)
Знак интеграла нельзя вынести из-под знака суммы, так как ![]() зависит от п. Поэтому разобьем
область интегрирования на два участка от
зависит от п. Поэтому разобьем
область интегрирования на два участка от ![]() до
до ![]() и от
и от ![]() до
до ![]() . В первой области можно использовать
дипольное приближение (10.6), при котором
. В первой области можно использовать
дипольное приближение (10.6), при котором ![]() не
зависит от q. Тогда при
не
зависит от q. Тогда при ![]() имеем
имеем
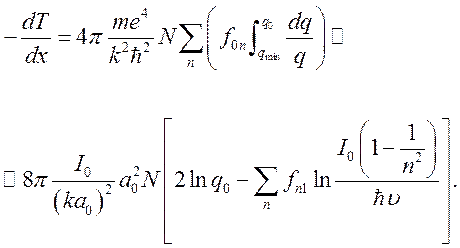 (10.8)
(10.8)
В противоположном предельном случае ![]() получим
получим
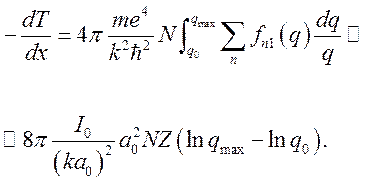 (10.9)
(10.9)
Сложив (10.8) и (10.9), получим
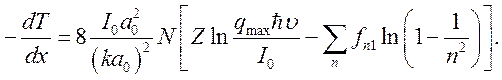 (10.10)
(10.10)
Введем некоторую среднюю энергию возбуждения ![]() ,
определяемую формулой
,
определяемую формулой
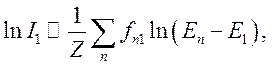
что позволяет потери представить в виде
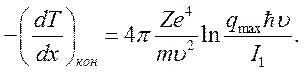 (10.11)
(10.11)
В дальнейшем мы будем называть потери (10.11) ионизационными.
Напомним, что здесь под тимеется в виду
масса электрона. В данную формулу входит всего одна характерная для атома
постоянная ![]() . Для атома водорода она равна
. Для атома водорода она равна ![]()
Таким образом, потери в (10.11) представлены как функция максимального импульса, который можно передать электрону атома при столкновении.
Рассмотрим торможение быстрого электрона. Когда
первичный и вторичный электроны приобретают после столкновения сравнимые
энергии, необходимо учитывать обменные эффекты. Поэтому при передаваемой
энергии, меньшей некоторого значения ![]() , можно
использовать (10.11), а при передаче от
, можно
использовать (10.11), а при передаче от ![]() до
до
![]() воспользуемся выражением (7.36):
воспользуемся выражением (7.36):
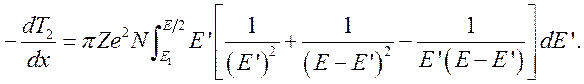 (10.12)
(10.12)
Величина ![]() связана
с
связана
с ![]() простым соотношением
простым соотношением ![]() . С учетом данного обстоятельства,
складывая (10.11) и (10.12), для потерь электрона получим
. С учетом данного обстоятельства,
складывая (10.11) и (10.12), для потерь электрона получим
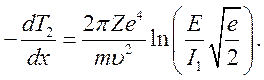
Отметим, что при рассеянии позитрона на атоме обменные
эффекты не работают и ![]() можно найти из условия
можно найти из условия ![]() , т.е.
, т.е. ![]() . Тогда из (10.11)
. Тогда из (10.11)
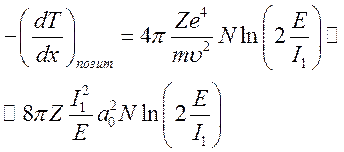 (10.13)
(10.13)
Для оценки тормозной способности ионов можно
воспользоваться формулой (10.11), в которую не входит масса рассеивающейся
частицы. Остается сосчитать ![]() , которое
согласно (7.42) равно
, которое
согласно (7.42) равно ![]() . С учетом данного
соотношения получим
. С учетом данного
соотношения получим
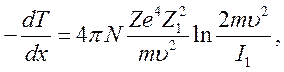 (10.14)
(10.14)
где ![]() — заряд рассеивающейся частицы.
— заряд рассеивающейся частицы.
Сравнение (10.13) и (10.14) показывает, что легкие и тяжелые частицы при одинаковой скорости теряют энергию на единицу пути одинаково. При сравнении потерь частиц с одинаковой энергией потери тяжелой частицы резко возрастают:
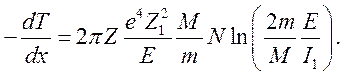 (10.15)
(10.15)
Для оценки потерь энергии быстрых релятивистских
частиц воспользуемся следующим приближением [4]. Пусть частица с зарядом ![]() пролетает вдоль оси x со скоростью
пролетает вдоль оси x со скоростью ![]() на расстоянии
на расстоянии ![]() от электрона атома, который мы будем
рассматривать как свободный. Тогда, предполагая, что скорость частицы
изменяется слабо, т.е. остается приблизительно постоянной:
от электрона атома, который мы будем
рассматривать как свободный. Тогда, предполагая, что скорость частицы
изменяется слабо, т.е. остается приблизительно постоянной: ![]() . Основное возмущение
направлено перпендикулярно
. Основное возмущение
направлено перпендикулярно ![]() и приводит к
формированию перпендикулярного импульса
и приводит к
формированию перпендикулярного импульса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.