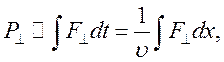 (10.16)
(10.16)
где ![]() .
.
Для расчета интеграла в (10.16) воспользуемся
следующими соображениями. Рассмотрим бесконечный цилиндр радиусом ![]() и применим к нему теорему Гаусса,
предполагая, что при х = 0 в центре находится заряд Ze:
и применим к нему теорему Гаусса,
предполагая, что при х = 0 в центре находится заряд Ze:
![]()
Учитывая, что ![]() , получим
, получим
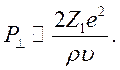 (10.17)
(10.17)
Величина переданной энергии оценивается
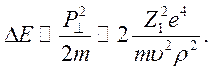 (10.18)
(10.18)
В указанном приближении потери энергии можно представить в виде
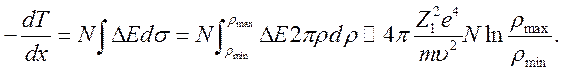 (10.19)
(10.19)
Найдем пределы интегрирования ![]() и
и ![]() .
.
Рассмотренная модель предполагала неподвижный заряд,
на котором рассеивается пролетающая частица. Это означает, что за время
взаимодействия ![]() электрон в атоме должен
оставаться неподвижным, т.е.
электрон в атоме должен
оставаться неподвижным, т.е. ![]() .
.
В п. 1.1 было показано, что классическая частота
вращения электрона в атоме порядка частоты излучаемого атомом фотона, т.е. ![]() . Отсюда получаем
. Отсюда получаем ![]() .
.
Отметим, что если ранее решение не зависело от приближения скорости
частицы к скорости света с, то при нахождении ![]() это
имеет принципиальное значение. Распределение поля зависит от скорости. С
увеличением
это
имеет принципиальное значение. Распределение поля зависит от скорости. С
увеличением ![]() поле сжимается и оказывается локализовано
в области
поле сжимается и оказывается локализовано
в области ![]() , где
, где ![]() ,
что приводит к уменьшению времени взаимодействия
,
что приводит к уменьшению времени взаимодействия ![]() .
В релятивистском случае
.
В релятивистском случае
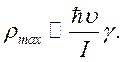 (10.20)
(10.20)
При
нахождении ![]() учтем, что
учтем, что ![]() и
и
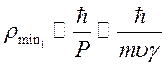 (10.21)
(10.21)
Отметим, что во всех рассмотренных выражениях фигурирует масса рассеянного электрона, так как динамика рассеяния определяется приведенной массой, которая определяется легкой частицей.
Для оценки ![]() необходимо также
учитывать, что электрону не может быть передана скорость более
необходимо также
учитывать, что электрону не может быть передана скорость более ![]() , т.е. энергия
, т.е. энергия ![]() . Подставляя
. Подставляя ![]() в (10.18),
получим в нерелятивистском случае
в (10.18),
получим в нерелятивистском случае
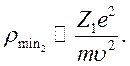 (10.22)
(10.22)
В релятивистском случае, приравнивая переданный
импульс ![]() к его значению в (10.17), получим
к его значению в (10.17), получим
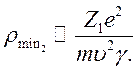 (10.23)
(10.23)
Очевидно, что ![]() определяется
из условия
определяется
из условия ![]() Причем, учитывая
Причем, учитывая
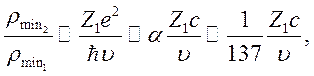
видим, что при ![]() определяется квантовыми
эффектами (10.21).
определяется квантовыми
эффектами (10.21).
Таким образом, окончательно получим
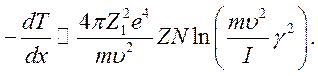 (10.24)
(10.24)
Подчеркнем, что в (10.24) не входят масса и энергия налетающей частицы, т.е. потери энергии, как и в (10.14), определяются только скоростью.
Для рассеяния электронов в ультрарелятивистском случае при точном расчете можно получить
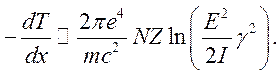
Следовательно, при большой анергии ![]() потери возрастают
потери возрастают ![]() .
.
Кратко подытожим сравнительные потери электронов и протонов. В нерелятивистском случае:
1.При одинаковых скоростях
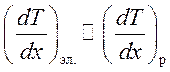
2. При одинаковых энергиях потери протонов в ![]() раз больше.
раз больше.
При ![]() потери определяются
значением параметра
потери определяются
значением параметра ![]() под знаком логарифма и
практически не зависят от энергии. Так, при Е = 10 ГэВ имеем
под знаком логарифма и
практически не зависят от энергии. Так, при Е = 10 ГэВ имеем
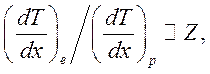
т.е. различие масс практически не играет роли.
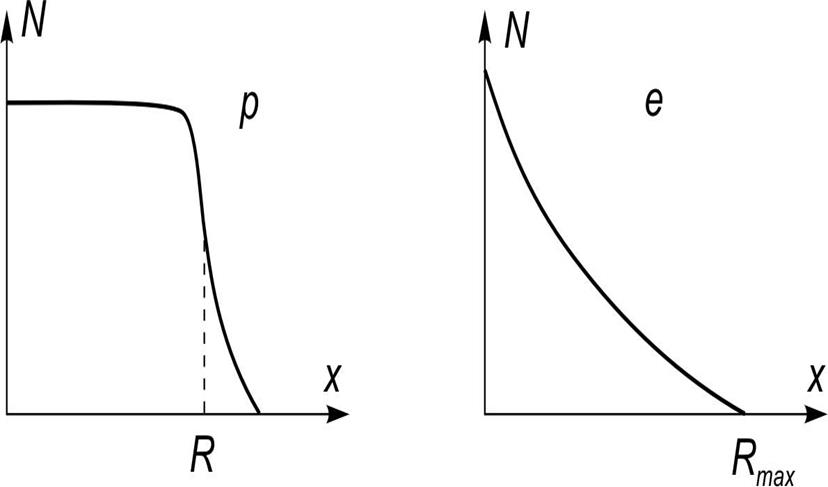
Ранее в п. 10 были рассмотрены потери энергии на единицу пути одной частицы без учета ее реальной траектории в веществе. При анализе движения пучка необходимо учитывать эффект рассеяния, т.е. тот факт, что траектории электронов не будут прямолинейны. Зависимость числа частиц, прошедших через слой вещества толщиной х, для электронов (е) и тяжелых частиц (р) качественно показаны на рис. 9.

Тяжелые частицы
мало рассеиваются, и все проходят толщину, равную пробегу ![]() . Для электронов из-за рассеяния, в том
числе и на большие углы, число частиц монотонно убывает с расстоянием. Поэтому
для электронов вводятся две величины: максимальный пробег и средний пробег. Как
было показано, удельные потери резко возрастают при уменьшении скорости.
. Для электронов из-за рассеяния, в том
числе и на большие углы, число частиц монотонно убывает с расстоянием. Поэтому
для электронов вводятся две величины: максимальный пробег и средний пробег. Как
было показано, удельные потери резко возрастают при уменьшении скорости.
Учитывая, что
число тяжелых частиц с расстоянием не уменьшается, то ионизационные потери
нарастают (рис. 10). Для электронов подобного пика не 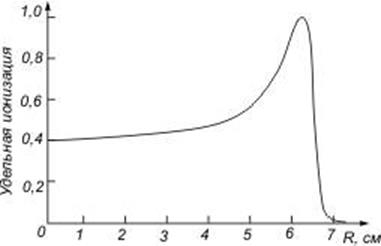 наблюдается. С
ростом энергии удельные потери на расстоянии
наблюдается. С
ростом энергии удельные потери на расстоянии ![]() сначала убывают
сначала убывают ![]() , а затем при
, а затем при ![]() нарастают
нарастают
![]() .
.

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.