Рассмотрим
процесс, в котором начальное состояние содержит атом в i-состоянии
и падающий фотон с энергией ![]() , а конечное — с атомом
в j-состоянии и фотоном с энергией
, а конечное — с атомом
в j-состоянии и фотоном с энергией ![]() [4].
[4].
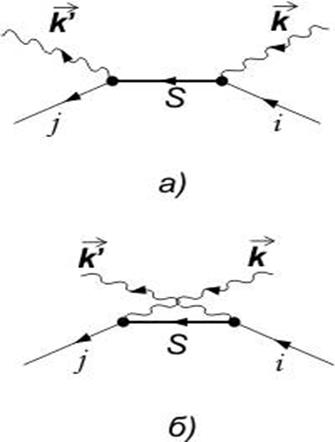 Процесс
(а) (рис. 2) включает поглощение падающего кванта, и затем испускание
конечного. В промежуточном состоянии квантов нет, атом же находится в
промежуточном (виртуальном) состоянии s с энергией
Процесс
(а) (рис. 2) включает поглощение падающего кванта, и затем испускание
конечного. В промежуточном состоянии квантов нет, атом же находится в
промежуточном (виртуальном) состоянии s с энергией ![]() . В другом способе (б)
атом сначала испускает конечный квант, а затем поглощает начальный.
Промежуточное состояние включает атом и два кванта и имеет энергию
. В другом способе (б)
атом сначала испускает конечный квант, а затем поглощает начальный.
Промежуточное состояние включает атом и два кванта и имеет энергию
![]()
 Эксперименты
показывают, что при облучении среды наблюдается рассеяние света, длина которого
содержит различные компоненты:
Эксперименты
показывают, что при облучении среды наблюдается рассеяние света, длина которого
содержит различные компоненты:
а) совпадающие
с длиной волны падающего света (релеевское рассеяние на атомах) и ![]() ;
;
б) отличающиеся от падающего на величину энергии кванта, характеризующего переходы в атоме
![]()
Различают две
компоненты рассеянного излучения: стоксову ![]() и
антистоксову
и
антистоксову ![]()
Вероятность процесса
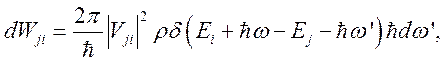 (4.1)
(4.1)
где ![]() – плотность
конечных состояний
– плотность
конечных состояний
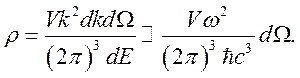
Матричный элемент процесса определяется вторым порядком теории возмущений [1, 2, 4]:
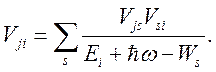 (4.2)
(4.2)
Для оценки матричных элементов используем эффективное дипольное взаимодействие:
![]() и
и 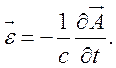
Используя координатную зависимость компонент электрического поля (см. раздел 2.2), получим
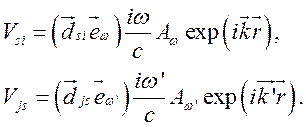 (4.3)
(4.3)
Подставляя
(4.3) в (4.2) и учитывая два возможных канала рассеяния с ![]() и
и ![]() , для
матричного элемента получим
, для
матричного элемента получим
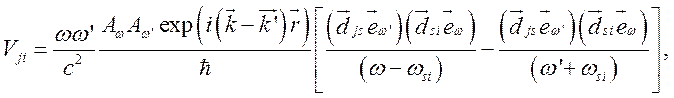 (4.4)
(4.4)
где 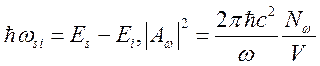 и
и 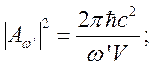 т.е.
т.е. ![]() -
рассеян один фотон.
-
рассеян один фотон.
Для нахождения
эффективного сечения рассеяния кванта в элемент телесного угла ![]() нужно вероятность
нужно вероятность ![]() (4.1)
проинтегрировать по энергии
(4.1)
проинтегрировать по энергии ![]() и воспользоваться
соотношением
и воспользоваться
соотношением
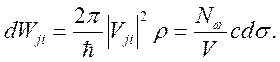 (4.5)
(4.5)
Здесь ![]() –
плотность потока налетающих фотонов.
–
плотность потока налетающих фотонов.
Из (4.5) с учетом (4.1) и (4.4) получим соотношение:
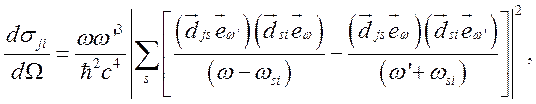 (4.6)
(4.6)
называемое дисперсионной формулой Крамерса – Гейзенберга.
При
приближении к резонансу ![]() сечение (4.6)
неограниченно растет. Как и при рассмотрении поглощения (2.12), необходимо
учитывать естественную ширину уровней, т.е. сделать замену
сечение (4.6)
неограниченно растет. Как и при рассмотрении поглощения (2.12), необходимо
учитывать естественную ширину уровней, т.е. сделать замену ![]() . Тогда главный (резонансный) член сечения
(4.6) примет вид:
. Тогда главный (резонансный) член сечения
(4.6) примет вид:
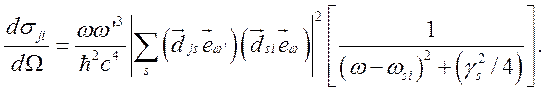 (4.7)
(4.7)
Здесь
суммирование по состояниям системы ![]() , имеющим энергию
, имеющим энергию ![]() (например, по проекциям момента).
(например, по проекциям момента).
Полное
резонансное поперечное сечение ![]() получается из (4.7)
посредством интегрирования по телесному углу
получается из (4.7)
посредством интегрирования по телесному углу ![]() (определяемому
направлением волнового вектора рассеянного фотона) и суммирования вкладов двух
поляризаций
(определяемому
направлением волнового вектора рассеянного фотона) и суммирования вкладов двух
поляризаций
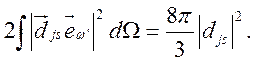 (4.8)
(4.8)
До сих пор при
вычислении рассматривалось рассеяние на одном атоме. В этом случае угол между ![]() и поляризацией
и поляризацией ![]() имеет
некоторое значение, случайным образом определенное в интервале
имеет
некоторое значение, случайным образом определенное в интервале ![]() . Для сравнения с экспериментом необходимо
учесть, что поток фотонов рассеивается на большом числе атомов и сечение
получается усредненное по всем возможным углам
. Для сравнения с экспериментом необходимо
учесть, что поток фотонов рассеивается на большом числе атомов и сечение
получается усредненное по всем возможным углам ![]() .
Учитывая, что при равновероятном распределении по углам
.
Учитывая, что при равновероятном распределении по углам ![]() среднее
значение
среднее
значение ![]() равно
равно ![]() ,
получим:
,
получим:
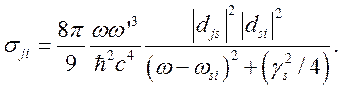 (4.9)
(4.9)
Напомним, что ![]() , где
, где
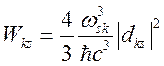 (4.10)
(4.10)
вероятность перехода с уровня s на уровень k.
С учетом (4.10) выражение (4.9) может быть записано в виде
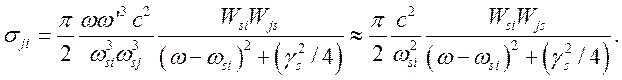 (4.11)
(4.11)
Здесь
использовано условие ![]() вблизи резонанса
вблизи резонанса ![]() и
и ![]()
Таким образом,
выражение (4.11) описывает полное сечение резонансной флуоресценции с
поглощением фотона с энергией ![]() , возбуждением атома из
состояния i в состояние s, последующим высвечиванием фотона
, возбуждением атома из
состояния i в состояние s, последующим высвечиванием фотона ![]() и переходом атома в состояние j. Полное сечение неупругого рассеяния можно получить из
(4.11) суммированием по всем конечным состояниям j,
лежащим ниже s.
и переходом атома в состояние j. Полное сечение неупругого рассеяния можно получить из
(4.11) суммированием по всем конечным состояниям j,
лежащим ниже s.
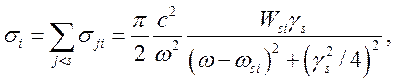
где ![]() и
и 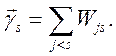
Рассмотрим случай
i = j и ![]() =
= ![]() . Примем также, что атом
первоначально находился в основном состоянии. Тогда из (4.11) резонансное
сечение
. Примем также, что атом
первоначально находился в основном состоянии. Тогда из (4.11) резонансное
сечение
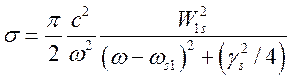 (4.12)
(4.12)
и, в случае точного резонатора ![]() , получим
, получим
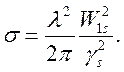 (4.13)
(4.13)
Отметим, что ![]() и, следовательно,
и, следовательно, ![]() –
частный вклад в ширину состояния s. Если s – первое возбужденное
состояние, то
–
частный вклад в ширину состояния s. Если s – первое возбужденное
состояние, то ![]() и
и ![]()
Таким образом, удивительные свойства резонансного рассеяния одинаково присущи как упругому, так и неупругому процессам.
Теперь рассмотрим
случай упругого рассеяния при энергии начального кванта ![]() ,
много большей энергии первого возбужденного состояния.
,
много большей энергии первого возбужденного состояния.
Простая оценка
полного сечения может быть получена из (4.6) в предположении ![]() и
и ![]() .
.
Тогда
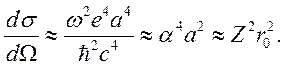
Точное выражение
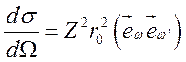 (4.14)
(4.14)
получим, используя (4.9), учитывая влияние всех уровней на рассеяние и применяя правило сумм осцилляторов [1, 2].
Рассмотрим
другой предельный случай, когда ![]() много меньше энергии
атомных переходов с основного состояния. Оценка сечения получается из (4.6),
если предположить, что
много меньше энергии
атомных переходов с основного состояния. Оценка сечения получается из (4.6),
если предположить, что ![]() и
и ![]() :
:
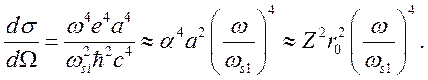 (4.15)
(4.15)
Точное выражение из (4.6) с суммированием вклада всех состояний может быть получено для атома водорода:
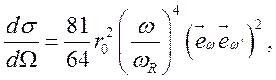 (4.16)
(4.16)
где ![]()
Рассмотренный случай описывает рассеяние фотонов оптических частот в газах. В частности, сильное рассеивание голубого цвета, т.е. больших частот, объясняет голубой цвет неба и красный цвет солнца на закате.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.