1.3. Релятивистские поправки к уровням энергии
Учет релятивистского электромагнитного взаимодействия мы начнем с анализа тонкой структуры атома водорода.
В [4]
проведено подробное изучение релятивистских эффектов и показано, что для
водорода поправка к гамильтониану порядка ![]() может
быть представлена в виде:
может
быть представлена в виде:
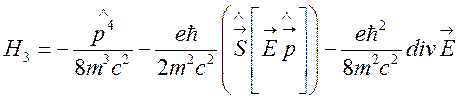 . (22)
. (22)
Первое слагаемое в (22) есть
следствие релятивистской зависимости кинетической энергии от импульса, то есть
разложения разности 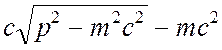 ; второе слагаемое — энергия
взаимодействия двигающегося магнитного момента с электрическим полем (спин-орбитальное
взаимодействие). Последнее слагаемое отлично от нуля в точках нахождения
зарядов, создающих внешнее поле.
; второе слагаемое — энергия
взаимодействия двигающегося магнитного момента с электрическим полем (спин-орбитальное
взаимодействие). Последнее слагаемое отлично от нуля в точках нахождения
зарядов, создающих внешнее поле.
Если электрическое поле центрально-симметрично, то
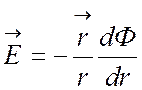 ,
(23)
,
(23)
и спин-орбитальное взаимодействие можно представить в виде:
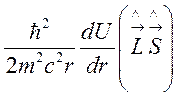 , (24)
, (24)
где ![]() —
оператор орбитального момента атома и U = eФ — потенциальная
энергия.
—
оператор орбитального момента атома и U = eФ — потенциальная
энергия.
Для атома
водорода с зарядом ядра Z поправки к энергии можно вычислить, используя
теорию возмущений 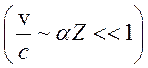 и принимая во внимание, что поле
ядра
и принимая во внимание, что поле
ядра 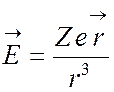 . Усреднение гамильтониана необходимо
проводить по нерелятивистским волновым функциям. Среднее значение оператора
. Усреднение гамильтониана необходимо
проводить по нерелятивистским волновым функциям. Среднее значение оператора ![]() можно найти, воспользовавшись соотношением:
можно найти, воспользовавшись соотношением:
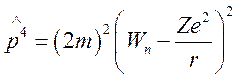 ,
,
где 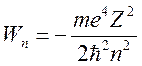 -
энергия невозмущенного уровня.
-
энергия невозмущенного уровня.
Таким образом,
задача сводится к расчету средних значений величин ![]() (где k
= -1; -2;
-3), который проведен в [1, §36]. Окончательно получим, что учет только
релятивистской зависимости энергии приводит к добавке:
(где k
= -1; -2;
-3), который проведен в [1, §36]. Окончательно получим, что учет только
релятивистской зависимости энергии приводит к добавке:
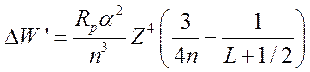 , (25)
, (25)
где 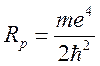 —
постоянная Ридберга,
—
постоянная Ридберга, 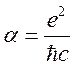 — постоянная тонкой структуры.
— постоянная тонкой структуры.
Спин-орбитальное взаимодействие вносит добавку энергии
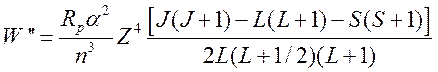 . (26)
. (26)
Здесь использовано
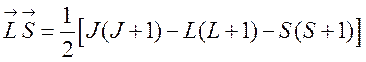 .
.
Полная энергия уровня получится,
если к значению нулевого приближения (7) добавить поправки ![]() Учитывая, что S = 1/2 и L = J ± 1/2,
независимо от знака энергия уровня равна
Учитывая, что S = 1/2 и L = J ± 1/2,
независимо от знака энергия уровня равна
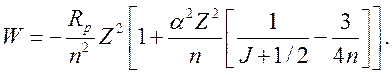 (27)
(27)
Напомним, что
в нулевом приближении (7) имеет место как вырождение энергетических состояний
по направлениям спина, так и кулоновское вырождение по L.
Спин-орбитальное взаимодействие снимает это вырождение, но не полностью —
остаются двукратно взаимно-вырожденные уровни с одинаковыми n и J,
но разными ![]() Уровень с главным квантовым числом n
расщепляется на n компонент тонкой структуры.
Уровень с главным квантовым числом n
расщепляется на n компонент тонкой структуры.
Необходимо отметить, что в случае атома водорода вырождение по L снимается так называемыми радиационными поправками (лембовский сдвиг), не учитываемыми уравнением Дирака [4]. В случае многоэлектронных атомов, как мы видели в разделах 1.1 и 1.2, вырождение по L снимается гораздо более сильным электростатическим взаимодействием между электронами.
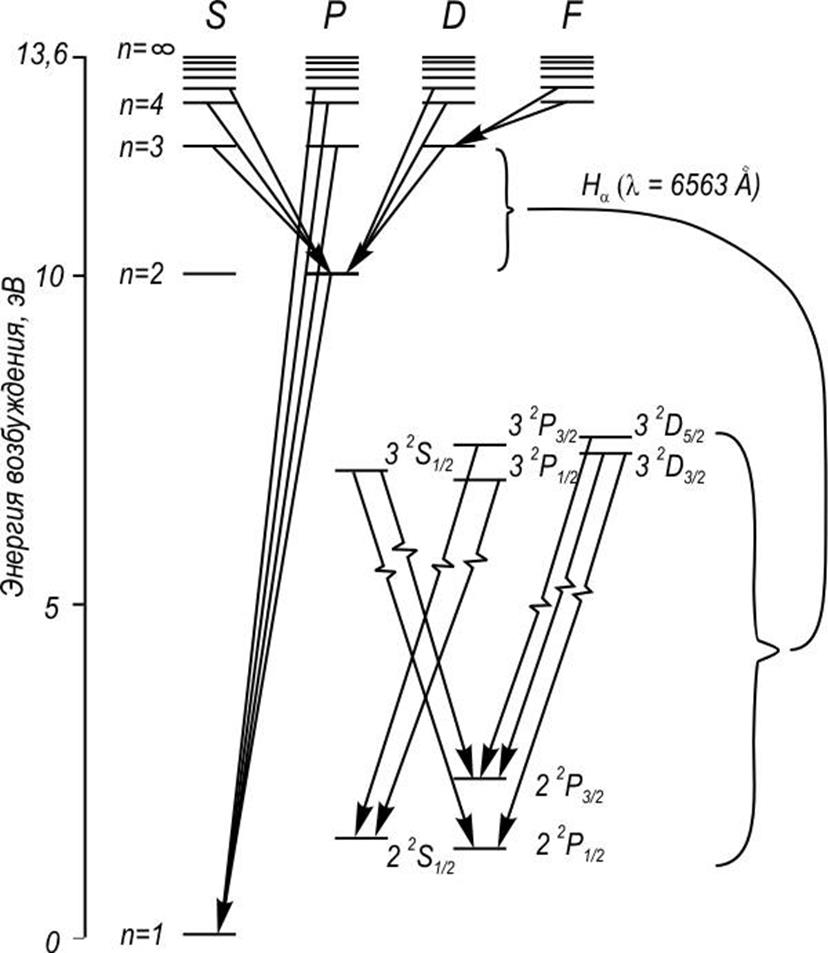
Таким образом, последовательность водородных уровней с учетом тонкой структуры такова:
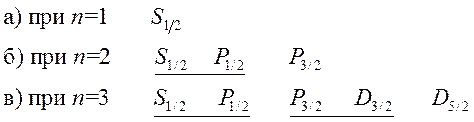
Подчеркнуты термы, вырождение которых снимает лембовский сдвиг. Схема энергетических уровней Н, демонстрирующая тонкую структуру приведена на рис. 3.
Полумодельно учет спин-орбитального взаимодействия может быть продемонстрирован следующим образом.
Электрон, движущийся в поле ядра, испытывает действие магнитного поля
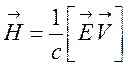 ,
(28)
,
(28)
где 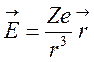 —
электрическое поле ядра. Учитывая, что
—
электрическое поле ядра. Учитывая, что 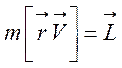 —
орбитальный момент, формулу (28) перепишем в виде:
—
орбитальный момент, формулу (28) перепишем в виде:
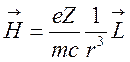 . (29)
. (29)
Добавочная
энергия, которую приобретает электрон с моментом ![]() в поле
в поле ![]() , равна
, равна
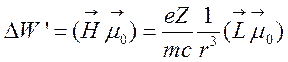 , (30)
, (30)
где 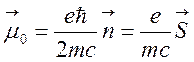 ,
, 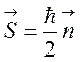 .
.
Таким образом, получим:
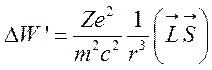 (31)
(31)

Как показано в
[4], учет релятивистских эффектов изменяет эту величину в 2 раза. Необходимо
также для ![]() вычислить среднее значение, то есть:
вычислить среднее значение, то есть:
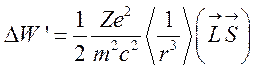 .
.
Используя радиальные волновые функции водородоподобного атома, легко показать[1], что
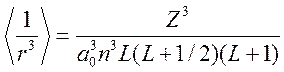 , (32)
, (32)
где 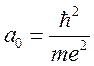 .
.
Таким образом, (31) можно представить в виде:
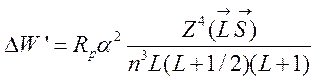 . (33)
. (33)
Учитывая, что ![]() , получим
, получим 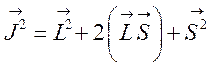 или
или
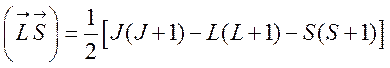 .
.
Подставляя значение 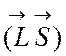 в (33) найдем добавку энергии
в (33) найдем добавку энергии
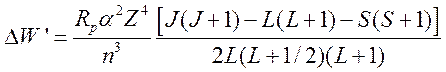 ,
,
совпадающую с точным расчетом (26).
В действительности, в сложных атомах релятивистские члены в гамильтониане распадаются на две категории — одни из них линейны относительно операторов спинов электронов, а другие квадратичны. Первые соответствуют орбитальному взаимодействию, вторые отвечают взаимодействию между спинами. Все они имеют одинаковый порядок по V/с.
Для взаимодействия спинов электронов в атоме имеем [3]
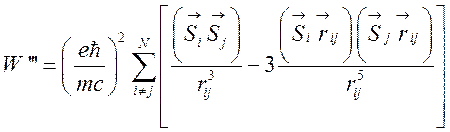 (34)
(34)
Фактически,
однако, в сложных атомах взаимодействия спин — орбита значительно превышает
взаимодействие спин — спин. Дело в том, что энергия спин-орбитального
взаимодействия, как видно из (27), отличается от основной энергии множителем ![]() . Этот коэффициент быстро растет с
увеличением атомного номера и в тяжелых атомах становится порядка единицы.
Коэффициент, определяющий поправку к энергии, обусловленную спин-спиновым взаимодействием,
не зависит от Z и его влиянием на энергию уровня можно пренебречь.
. Этот коэффициент быстро растет с
увеличением атомного номера и в тяжелых атомах становится порядка единицы.
Коэффициент, определяющий поправку к энергии, обусловленную спин-спиновым взаимодействием,
не зависит от Z и его влиянием на энергию уровня можно пренебречь.
Для атома с числом электронов N энергия спин-орбитального взаимодействия равна
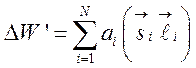 , (35)
, (35)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.