Релятивистские поправки к уровням энергии (Раздел 1.3. учебного пособия), страница 2

где коэффициент , согласно (26), должен зависеть от n и . Усреднение выражения (35) по невозмущенным волновым функциям (полученным в нулевом приближении) приводит к тому, что среднее значение 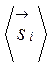 направлено по -полному спину атома, а 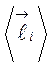 — по -полному моменту. В результате получим:

,                                           (36)

где А — постоянная для данного терма, зависящая только от L и S, но не зависящая от полного момента J. Аналогично (26) имеем:

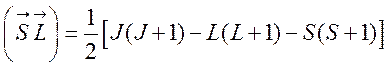 .                          (37)

Таким образом, в результате релятивистских эффектов уровень с данными значениями L и S расщепляется на ряд уровней с различными значениями J. Об этом расщеплении говорят как о тонкой структуре или мультиплетном расщеплении уровня. Известно, что J пробегает значения от L + S до , поэтому уровень с данным L и S расщепляется на 2S + 1 (если L > S) или  2L+ 1 (если S > L) различных уровней. Каждый из этих уровней остается вырожденным относительно направления , т.е. 2J +  1 раз.

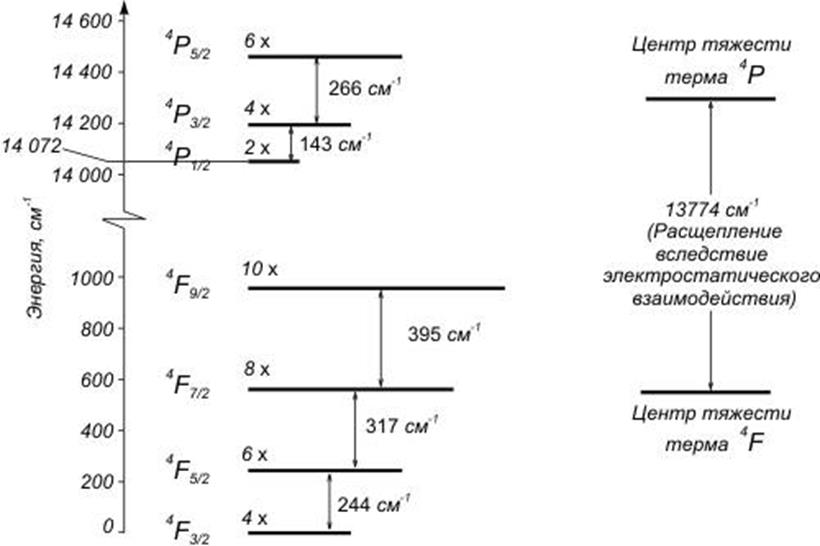
Важно, что мультиплетное расщепление уровней с разными J происходит на фоне электростатического взаимодействия, величина которого зависит от значений орбитального момента L и спина S. В качестве примера, демонстрирующего как электростатическое, так и релятивистское электромагнитное взаимодействие, на рис. 4 приведена схема уровней трехзарядного иона хрома , имеющего на своей верхней (3d) оболочке 3 электрона. Его основным термом является , т.е. L = 3 и S = 3/2. Возможные значения J = 9/2; 7/2; 5/2 и 3/2 (от J = L + S до J = L - S). Мультиплетное расщепление показано на рис. 4. На этом же рисунке показан терм  с L = 1 и S = 3/2. Различие энергии термов  и  обусловлено электростатическим взаимодействием, которое в ~ 40 раз превышает спин-орбитальное. Терм  может иметь J = 1/2; 3/2 и 5/2 и расщепляется на три подуровня.

Необходимо отметить, что точность выполнения рассмотренных закономерностей мультиплетного расщепления может быть легко проверена экспериментально. Формула (36), с учетом (37), определяет добавку к энергии невозмущенного состояния. Поэтому расстояние между соседними подуровнями с различными J определяется выражением

.                           (38)

Соотношение (38) является правилом интервалов. Причем, отношение двух интервалов уже не зависит от трудно определяемой константы А

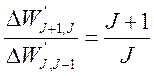.                                               (39)

Например, рассмотрим терм   (S =2 и L =2), для которого J может принимать значения J = 0,1; 2; 3; 4. Интервалы будут относиться

; ; .

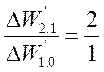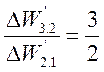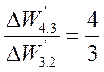Это обусловлено следующим. Изложенная в данном разделе схема построения атомных уровней основана на представлении, что в нулевом приближении можно ввести понятие орбитального момента электронов , которые складываясь определяют полны момент , а спины  определяют полный . Такое рассмотрение возможно при условии малости релятивистских эффектов, т.е. малости мультиплетного расщепления по сравнению с разностью уровней с различными  и . Это приближение называется рассель-саудоровским или ( - ) типом связи.Эта схема сложения моментов предполагает что взаимодействие орбитальных моментов между собой и спиновых моментов между собой намного больше, чем взаимодействие спина и орбитального момента каждого электрона. Важно отметить, что зависимость энергии как от , так и отопределяется электростатическим взаимодействием, что было продемонстрировано ранее при анализе энергетических уровней атома гелия (см. раздел 1.2).

            У тяжелых атомов может реализоваться противоположный предельный случай, когда энергия спин-орбитального злектромагнитного взаимодействия становиться больше изменения электростатической энергии в зависимости от  и . В этом случае нельзя говорить о  и  в отдельности. Строго говоря, сохраняется только  - полный момент атома как замкнутой системы. Сильное спин-орбитальное взаимодействие для каждого электрона приводит к тому, что каждый электрон характеризуется момметом , которые складываясь, образуют полный момент. Например терм атома для случая двух электронов обозначается символом .

Сравнение с экспериментом показывает, что правило интервалов, например, для атомов Mg, Ca, Sr, Zn, выполняется с точностью до 2,5 %, тогда как для тяжелых элементов, например Hg, точность уменьшается до ~ 30%.

Рис.4. Квартет энергетических уровней свободного трехзарядного иона хрома Cr3+ (3d3)

Уровни соответствуют системе трех электронов в 3d-оболочке. Расщепление между термами  и  связано с электростатическим отталкиванием между электронами. Расщепления между уровнями с различными значениями J в пределах каждого терма вызваны спин - орбитальным взаимодействием.

Энергетический диапазон между термами электронной конфигурации  составляет 14000 - 37000 . Следующие уровни, принадлежащие электронной конфигурации 3d²4s, расположены выше на 100000 .

Расмотрим случай одного р- и одного d- электронов, тогда получим

;

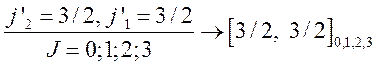 и т. д.