Релятивистские поправки к уровням энергии

Лекция 3

(Берестецкий, с 153)

Для атома водорода поправка к гамильтониану порядка  :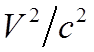

;

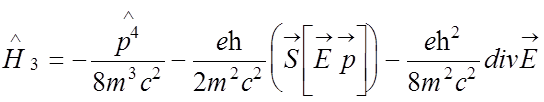Первый член – релятивистская зависимость энергии от импульса.

Второй – спин-орбитальное взаимодействие. Его можно представить в виде:

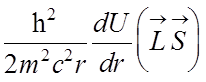
Среднее значение оператора  можно найти из нерелятивистского УШ:

(Ландау  стр.150)

                                           __    _______________

,

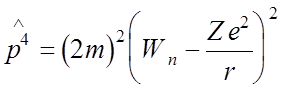где 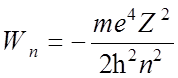     - энергия невозмущенного уровня.

Учет только релятивистской зависимости энергии приводит к добавке:

,

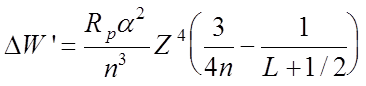где 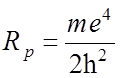   - постоянная Ридберга,  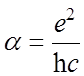     - постоянная тонкой структуры.

Спин-орбитальное взаимодействие вносит добавку энергии:

                  

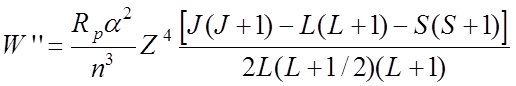
Здесь использовано :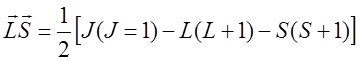

В результате для S = 1/2   и   L = J ± 1/2  полная энергия уровня равна (тонкая структура)

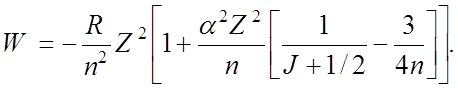
Последовательность уровней атома H с учетом тонкой структуры:

           

                  

подчеркнутые термы остаются вырожденными в рамках модели релятивистских поправок. Их вырождение снимается в результате учета радиационных поправок (лэмбовский сдвиг).

 

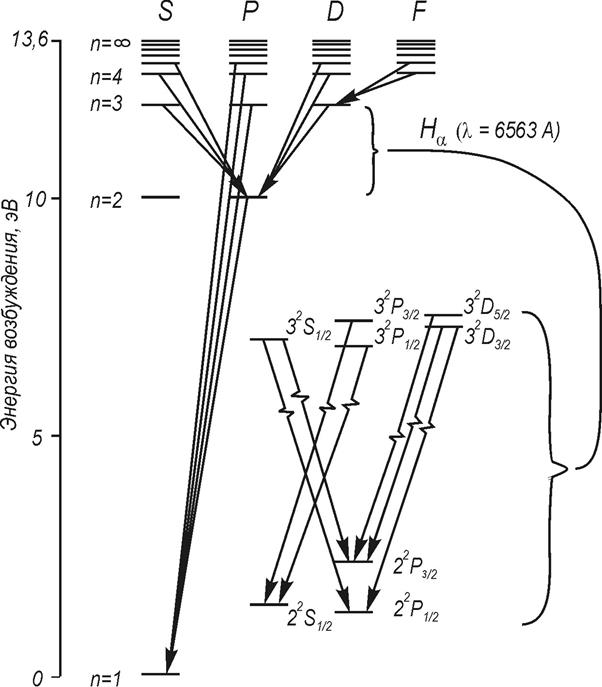
Пример тонкого расщепления уровней для линии Н_α приведен на диаграмме Гротриана для водорода

 

Для атома с числом электронов N  энергия спин - орбитального взаимодействия равна:

,

 .

.

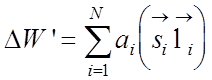
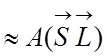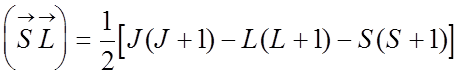Мультиплетное расщепление:

Таким образом, в результате релятивистских эффектов уровень с данными значениями L  и S  расщепляется на ряд уровней с различными значениями  J.  Об этом расщеплении говорят как о тонкой структуре или мультиплетном расщеплении уровня.

Уровень с данным L и S расщепляется на 2S+1 (при L>S) или на 2L+1 (при S>L) подуровней. Каждый из этих уровней остается вырожденным относительно направления , т.е.  2J+1 раз.

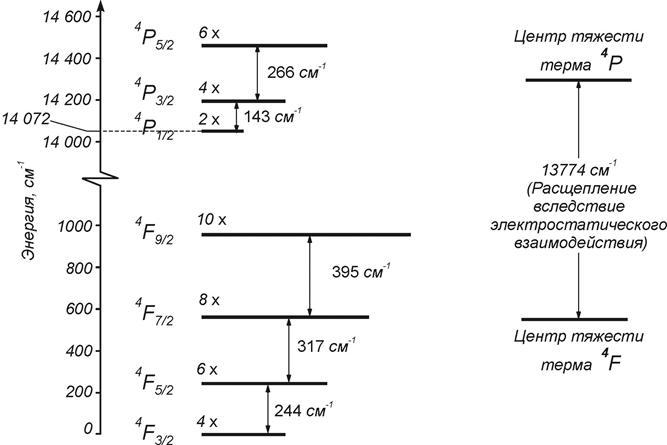
Сравнение электростатического  и электромагнитного взаимодействий в атоме на примере Cr.³⁺   (3d³ )

Правило интервалов Ланде: расстояние между соседними подуровнями с различными J равно

,

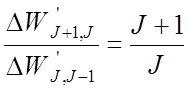
Пример:    терм  ⁵D_J    (S = 2  и  L = 2, J = 0, 1,2, 3, 4).

 Интервалы относятся:  

 ;   ;    . 

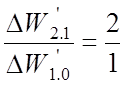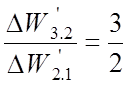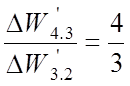Сравнение с экспериментом:

правило интервалов для атомов  Mg, Ca, Sr, Zn,  выполняется с точностью до 2,5 %, тогда как для тяжелых элементов, например Hg, точность уменьшается до ~ 30% .

Приближение центрально-симметричного поля в сложном атоме (одноэлектронное приближение)

Электростатическое взаимодействие электронов учитывается усредненным центрально-симметричным хартри-фоковским полем:

,

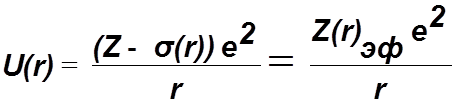Z_эф(r) – эффективный заряд ядра действующий на электрон на расстоянии r.

Два принципа построения электронных оболочек

принцип Паули:                      только один электрон в (n, , , 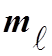m_s)- состоянии

принцип минимума энергии: из возможных состояний осуществляется состояние с минимальной энергией.

Энергия электрона (!) в атоме определяется: (Ельяшевич,194 и далее)

·  зарядом ядра Z –                            энергия понижаются с ростом Z

·  главным квантовым числом n–  энергия связи уменьшается с ростом n

·  орбитальным моментом –          энергия связи растет с уменьшением  при заданном n (проникающие орбиты).

·  взаимодействием электронов в подоболочке – при данном  энергия связи растет  для различных 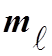 (орбиты пространственно разнесены)- правило Хунда (Бейзер, 209)

Последовательность заполнения оболочек

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 6d, 7s.

 

Максимальное число электронов в оболочке и подоболочке с данными n,

,    , →

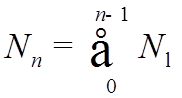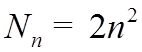
Оболочка	n	Максимальное число электронов                       в подоболочке					Всего электронов в оболочке
		s	p	d	f	g
К	1	2					2
L	2	2	6				8
M	3	2	6	10			18
N	4	2	6	10	14		32
O	5	2	6	10	14	18	50

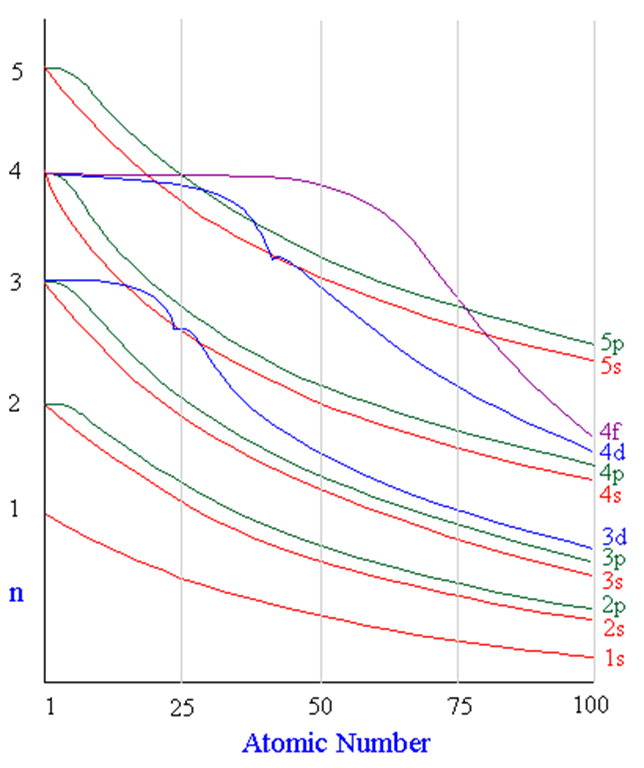
Зависимости энергий связи электронов от Z, n и

I

He– два 1s электрона,  Z = 2.  Энергия связи равна 24,8 эВ > 13,6 эВ для

 1s  электрона атома H (Z = 1) –                            эффект увеличения  Z .

Li –  Z = 3, третий электрон в 2s –состоянии, 5,4 эВ – эффект влияния n.

II

Be –( Z= 4;  9,3 эВ) и до Nе(Z = 10; 21,6 эВ) заполняются 2s и 2р-подоболочки.

При заданном  Z   и  n  оболочка с меньшим  расположена глубже, то есть s глубже р и т.д.                                                                         эффект понижения

 Однако с ростом Z энергия связи атомов растет (т.е. эффект Z преобладает).

III

Na – Z = 11 одиннадцатый электрон в 3s-состоянии.  Эффект изменения  n  и перехода на более высокую оболочку оказывается сильнее эффекта увеличения Z, и энергия связи верхнего электрона снова сильно падает. Отметим, что энергия связи внутренних 10 электронов в Na cущественно больше, чем в Ne.

          Такая картина заполнения электронных оболочек характерна для всей последовательности элементов, однако влияние  в тяжелых атомах становится существеннее.

Периодичность физико-химических свойств атомов

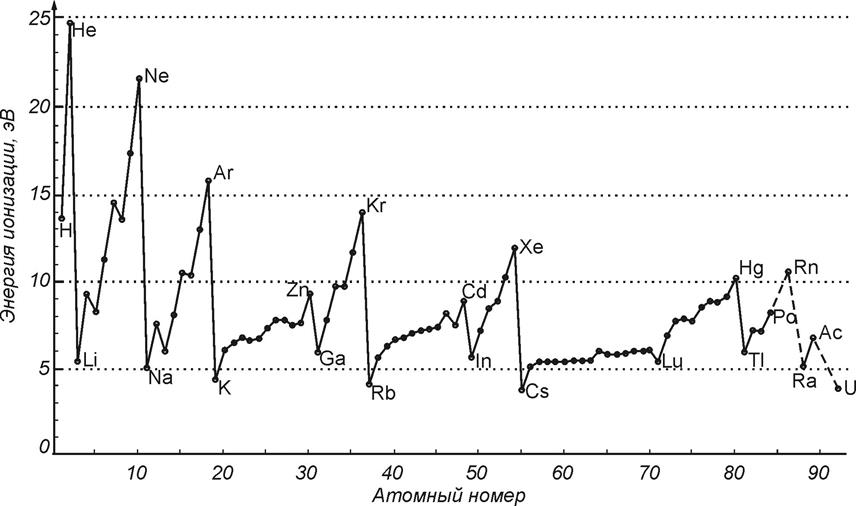
Потенциал ионизации

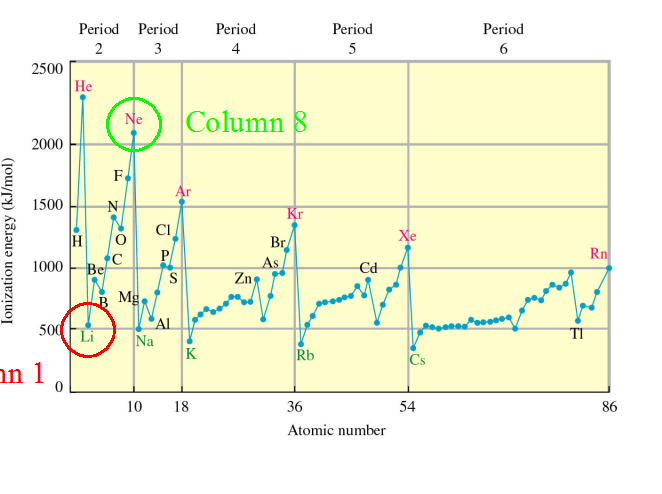
1 kJ/mol = .010364 eV/atom

Таблица Менделеева (1869)