Принцип возможных перемещений. Уравнения равновесия с множителями (элементы аналитической статики)

§ 1.11. Принцип возможных перемещений. Уравнения равновесия с множителями (элементы аналитической статики).

            А) Принцип возможных перемещений.

Механической системой называется множество материальных точек, выделенных для изучения и объединенных по некоторому принципу (Солнечная система, механические устройства и механизмы).

            Точки системы могут иметь те или иные стеснения своих движений, называемых связями.

1. Свободная точка, не имеющая связей, имеет три степени свободы, т.е. для описания ее положения необходимо задать три параметра x(t), y(t), z(t).
2. На свободную точка наложена одна связь – мы удерживаем ее с помощью невесомого стержня длины R. Один конец стержня шарнирно закреплен в точке О – начале координат. В этом случае координаты точки обязаны подчиняться уравнению x² + y² + z²=R² и мы говорим, что на точку наложена стационарная удерживающая связь, у нее осталось две степени свободы (точка может находиться на поверхности сферы радиуса R и ее положение можно описать с помощью двух параметров, например, двух углов).

В общем случае мы имеем механическую систему из n точек, каждая точка имеет три степени свободы, а вся механическая система, если на нее не наложено никаких связей, имеет 3n степеней свободы.

Ограничения на движение точек системы (связи) заданы независимыми между собой уравнениями:

f_j(x₁,y₁,z₁…..x_n,y_n,z_n) = 0        ( j = 1,2….s )

            Если число связей s равно 3n, то эти уравнения определяют 3n координат, система может иметь одно или несколько определенных положений и перемещаться не будет. Для возможности перемещения системы должно выполняться условие k = 3n – s > 0. Число k называют числом степеней свободы системы.

            Пусть к материальной точке М приложена сила F. Предположим, что точке М сообщено некоторое бесконечно малое не противоречащее уравнениям связей перемещение . Это перемещение назовем возможным в отличие от действительного , которое точка совершает на самом деле под действием приложенных сил.

            Элементарной работой силы F на возможном перемещении  называют величину

            У нас есть система точек M_i с координатами (x_i,y_i,z_i) и действующие на них силы (i=1,2…n). Точки системы стеснены некоторыми связями. По аксиоме о связях их действие можно заменить действием сил реакций  (i=1,2…n). То есть, добавив к силам F_i все реакции R_i систему точек можно мыслить свободной от связей, вызывающих реакции R_i.

Определение. Идеальными называются связи, работа сил реакций (i=1,2…n) которых на любых возможных при этих связях перемещениях равна нулю, то есть

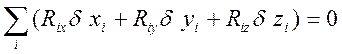   (1.11.1)

            Сформулируем основной принцип аналитической статики для систем с идеальными удерживающими стационарными связями. Система точек находится в состоянии равновесия, значит сумма проекций сил на все оси декартовой системы координат должны быть равны нулю:

F_ix+R_ix=0; F_iy+R_iy=0; F_iz+R_iz=0; (i = 1,2…n)

            Отсюда мы можем определить R_ix,R_iy,R_iz и подставив их в уравнение для определения  идеальных связей (1.11.1) получить выражение:

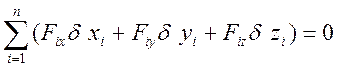    (1.11.2)

справедливое для произвольных возможных перемещений в положении равновесия рассматриваемой механической системы. Это и есть необходимое и достаточное условие равновесия механической системы, которое называется принципом возможных перемещений. Принцип возможных перемещений может быть взят за основу всех положений статики взамен набора аксиом, которые мы использовали с самого начала для вывода наших результатов.

            Б) Уравнения равновесия с множителями.

            Имеем уравнения связей f_j(x_i,y_i,z_i)=0 (i=1,2…n; j=1,2…s) и силы , действующие на точки механической системы.

            Из уравнений связей следует, что

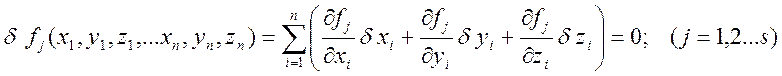            (1.11.3)