В положении равновесия должен также выполняться принцип возможных перемещений (1.11.2). Умножая каждое из s уравнений (1.11.3) на соответствующий неопределенный множитель lj сложим их с (1.11.2):
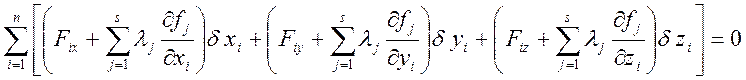 (1.11.4)
(1.11.4)
В этом соотношении 3n вариаций dxi, dyi, dzi. Из них s-зависимые, а k=3n-s – независимые. Подберем s множителей lj так, чтобы коэффициенты при s зависимых вариациях обращались в ноль. Этот подбор можно провести единственным образом, так как определитель из коэффициентов при зависимых вариациях в (1.11.3) отличен от нуля в силу того, что уравнения связей независимые.
При таком выборе s множителей lj в (1.11.4) останутся только вариации независимых переменных. Из-за произвольности последних и равенства нулю выражения (1.11.4) необходимо должны быть равны нулю коэффициенты и при этих вариациях. Таким образом, в положении равновесия механической системы должны обращаться в ноль все коэффициенты в (1.11.4):
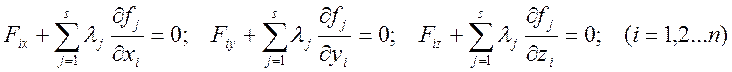 (1.11.5)
(1.11.5)
Добавив к этим 3n уравнениям s уравнений связей, мы сможем определить 3n+s неизвестных: lj (j=1,2…s) и xi,yi,zi (i=1,2…n).
 Пример 1. Рассмотрим
полиспаст, одно из простейших механических устройств, которое давно известно
человечеству, как и устройства вроде рычага и клина.
Пример 1. Рассмотрим
полиспаст, одно из простейших механических устройств, которое давно известно
человечеству, как и устройства вроде рычага и клина.
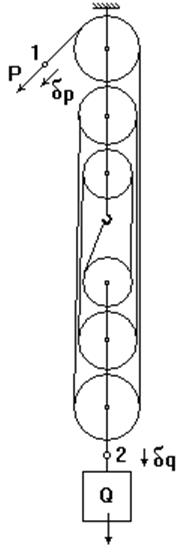
С точки зрения аналитической статики полиспаст представляет собой механическую систему, состоящую из двух точек 1 и 2, к которым приложены силы P и Q, все прочее относится к реализации связи между этими двумя точками.
Для нашего случая принцип возможных перемещений записывается так:
Pdp + Qdq = 0,
P = Q/6.
Это означает, что с помощью приведенной на рисунке конструкции полиспаста для удержания в равновесии груза весом Q необходимо приложить в 6 раз меньшую силу P.
 Пример 2. Рассмотрим
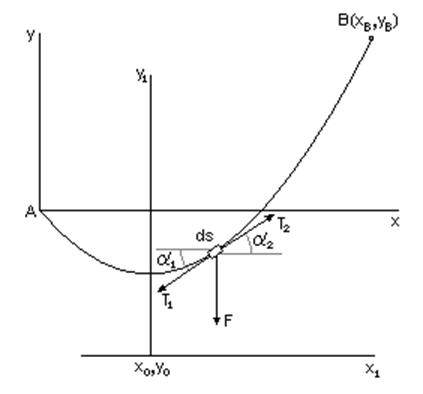
гибкую однородную тонкую тяжелую нить, закрепленную в точках A и B,
длина нити – l, линейная плотность - r.
Пример 2. Рассмотрим
гибкую однородную тонкую тяжелую нить, закрепленную в точках A и B,
длина нити – l, линейная плотность - r.
l2 > x2B + y2B
Рассмотрим элемент нити ds. Нить нерастяжимая, ds вдоль длины нити не меняется.
f º dx2 + dy2 + dz2 – ds2 = 0 (1.11.6)
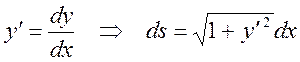 (1.11.6a)
(1.11.6a)
На элемент ds действует внешняя сила тяжести F=grds, направленная вертикально вниз. Элементарная работа этой силы на возможном перемещении dy равна grdsdy.
Для всей нити, находящейся в положении равновесия, имеем принцип возможных перемещений:
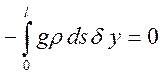
Рассматриваем плоский случай параллельных сил тяжести, (1.11.6) принимает вид:
f ºdx2 + dy2 – ds2 = 0
Отсюда можно получить
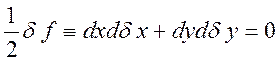 (1.11.7)
(1.11.7)
Используем метод неопределенных множителей Лагранжа: разделим (1.11.7) на ds и умножим на множитель l(x,y).
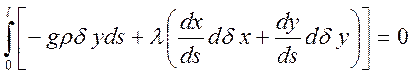 (1.11.8)
(1.11.8)
Перепишем это в виде: 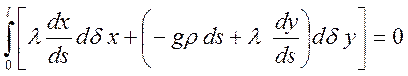
Интегрирование по частям и условия закрепления концов нити A и B дают:
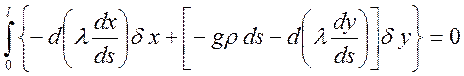
Мыслим здесь dy зависимой вариацией, а dx – независимой, тогда получаем:
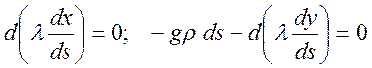 (1.11.9)
(1.11.9)
Выясним смысл множителя l. Условие равновесия элемента ds в проекции на вертикальную ось имеет вид (см.рис.):
![]()
или,
если учесть, что 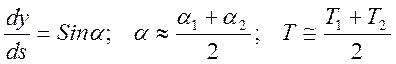
![]() или
или 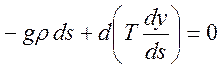 (1.11.10)
(1.11.10)
Сравнивая (1.11.9) и (1.11.10) видим, что T= - l, то есть условия равновесия нити выглядят следующим образом:
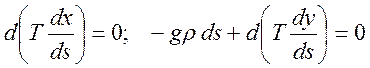 (1.11.11)
(1.11.11)
Из
первого соотношения (1.11.11) следует, что 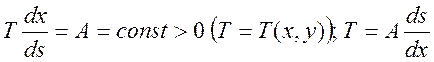 .
.
Тогда второе соотношение (1.11.11) можно переписать в виде:
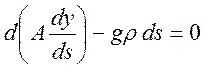 или
или ![]() ; (1.11.12)
; (1.11.12)
Учитывая (1.11.6a) и вводя обозначение Aºgra перепишем (1.11.12) в виде
![]()
В итоге получаем дифференциальное уравнение
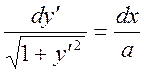 ; (1.11.13)
; (1.11.13)
Дважды интегрируя (1.11.13) получаем уравнение цепной линии
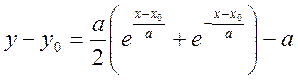 ; (1.11.14)
; (1.11.14)
Если ввести новые координаты x1=x-x0, y1=y-y0-a, то уравнение (1.11.14) принимает вид
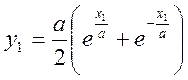 - уравнение
гиперболического косинуса.
- уравнение
гиперболического косинуса.
Из условий на концах нити A (x=0, y=0), B (x=xB, y=yB) и длины нити l можно получить
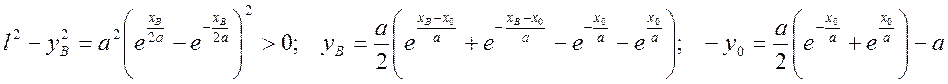
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.