Простейшие движения твердого тела. Скорости и ускорения точек тела при вращении. Плоское движение твердого тела

Простейшие движения твердого тела

§ 2.7.Степени свободы. Теорема о проекциях

Числом степеней свободы твердого тела называют число независимых параметров, определяющих положение тела относительно рассматриваемой системы координат.

Свободная точка имеет три степени свободы, свободное твердое тело в общем случае имеет шесть степеней свободы. Твердое тело (его положение) может быть задано тремя точками, не лежащими на одной прямой. Расстояния между точками в твердом теле должны оставаться неизменными при любых его движениях. Это накладывает на координаты фиксированных точек три условия. Получаем (3n-k=s)=(9-3=6) шесть степеней свободы.

Теорема.  При любом движении твердого тела проекции скоростей двух его точек на прямую, соединяющую эти точки, равны.

Возведем обе части в скалярный квадрат: Продифференцируем по времени:

            Раскладывая скалярные произведения векторов и сокращая на l, имеем: v_ACosa=v_BCosb

§ 2.8. Поступательное движение твердого тела

            Поступательным движением твердого тела называется такое его движение, при котором любая прямая, жестко связанная с телом, остается параллельной самой себе в каждый момент времени.

            Очевидно, достаточно, чтобы это выполнялось только для двух непараллельных прямых, связанных с телом.

            Траектории точек у поступательно движущегося твердого тела могут быть не только прямыми, но и любыми кривыми, в том числе окружностями.

            Теорема. При поступательном движении твердого тела траектории, скорости и ускорения всех точек тела одинаковы.

Вектор АВ является всегда постоянным по модулю, а при поступательном движении не изменяется и по направлению. При сдвиге на АВ траектории точек совпадут.

            Движение твердого тела, для которого векторы скоростей точек равны только в один момент времени, а не все время, называется мгновенным поступательным движением.

            Для мгновенного поступательного движения ускорения точек в общем случае не являются одинаковыми.

            Твердое тело, движущееся поступательно, имеет три степенм свободы, так как для описания его движения достаточно задать функции x=f₁(t), y=f₂(t), z=f₃(t) для любой точки и использовать кинематику одной точки.

§ 2.9. Вращение твердого тела вокруг неподвижной оси

            Вращением твердого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела (или его продолжения) остаются неподвижными в течение всего времени движения.

            Прямая, соединяющая эти точки, называется осью вращения.

Положение тела относительно выбранной системы отсчета полностью и однозначно определяется в любой момент времени, если задано уравнение , то есть у тела одна степень свободы. Угловая скорость , Угловое ускорение

            Вращение называется равномерным, если w=const

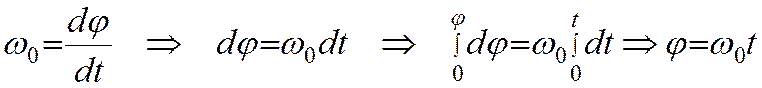
            Вращение называется равнопеременным, если e=const

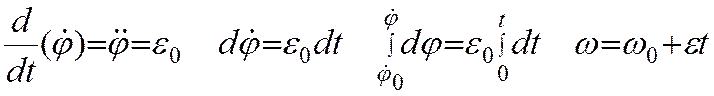
            и после второго интегрирования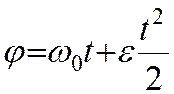  

§ 2.10. Скорости и ускорения точек тела при вращении

j = f(t),     s = hj Скорости точек тела при вращении вокруг неподвижной оси пропорциональны их расстояниям до этой оси и перпендикулярны радиусам вращения.

            Ускорение точки разлагаем на касательную и нормальные составляющие

            Касательные, нормальные и полные ускорения точек, как и скорости, распределены тоже по линейному закону.

            Обозначив a угол между полным ускорением точки и ее радиусом вращения, имеем:

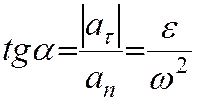
            так как нормальное ускорение a_n всегда положительно.

            Угол a для всех точек тела один и тот же. Откладывать его следует от ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения независимо от направления вращения твердого тела.

Пример

Кроме того,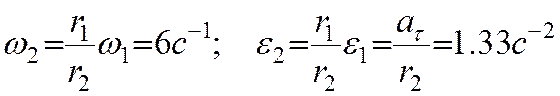  

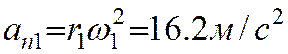
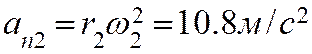
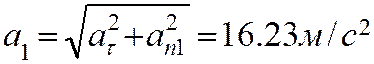
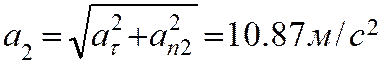
Для диска 1,2 (точка касания) получаем

Векторы угловой скорости и ускорения

- векторная формула Эйлера Из параграфа о сложном движении точки считая и равными нулю имеем и можем получить все предыдущие результаты для вращения тела вокруг неподвижной оси.

§ 2.11. Плоское движение твердого тела

            Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же неподвижной плоскости. Часто это движение называют плоскопараллельным, так как плоскости, в которых движутся отдельные точки, параллельны между собой.

            Траектории точек тела при плоском движении являются плоскими кривыми.

            Такой случай движения часто реализуется в технике при движении механизмов и машин.

            Вращательное движение твердого тела вокруг неподвижной оси является частным случаем плоского движения.

            Для изучения плоского движения твердого тела достаточно рассмотреть движение плоской фигуры в ее плоскости, параллельной неподвижной плоскости P₀.

            Для задания положения плоской фигуры на плоскости относительно координат Oxy достаточно задать на этой плоскости положение отрезка О'M, скрепленного с фигурой.

Скрепим с твердым телом подвижную систему осей O’x’y’ Тогда для координат (x,y) точки М будем иметь: где , a - постоянный угол между O’M и осью O’x’ Уравнения движения твердого тела в плоском движении будут иметь вид: xo’ =f1(t); yo’ =f2(t); j = f3(t), то есть имеем три степени свободы.

            Раскрывая Cos и Sin суммы и учитывая, что r’Cosa=x’, r’Sina=y’ получаем:

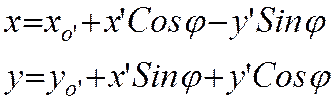
или в векторно-матричной форме

, где

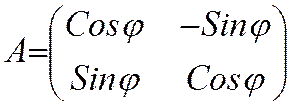 - матрица поворота на плоскости.

            Эти формулы позволяют определить координаты любой точки плоской фигуры по заданным уравнениям движения этой фигуры и координаты ее точки относительно подвижной системы координат, скрепленной с фигурой.