Примеры решения задач типового расчёта
по линейной алгебре и аналитической геометрии.
Задача 1.1. Вычислить![]() , представить ответ в алгебраической,
тригонометрической, показательной формах.
, представить ответ в алгебраической,
тригонометрической, показательной формах.
Решение. Представим
комплексное число в тригонометрической форме. Для этого находится его модуль:  , далее вычисляется аргумент комплексного
числа:
, далее вычисляется аргумент комплексного
числа: 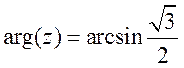 , либо
, либо 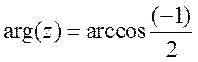 ,
наконец,
,
наконец,
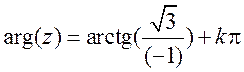 , где
, где ![]() , если комплексное число находится в первой
или четвертой четверти,
, если комплексное число находится в первой
или четвертой четверти, ![]() , если комплексное число
находится во второй или третьей четверти. В данном случае аргумент комплексного
числа равен:
, если комплексное число
находится во второй или третьей четверти. В данном случае аргумент комплексного
числа равен: 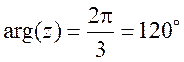 .
.
Поэтому тригонометрическая форма
имеет вид: 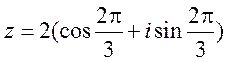 .
.
По формуле Муавра ![]() , где
, где ![]() -
аргумент комплексного числа
-
аргумент комплексного числа ![]() , получаем:
, получаем:
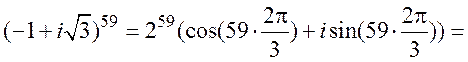
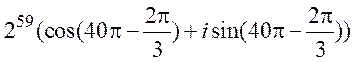 ,
,
окончательно: ![]() =
=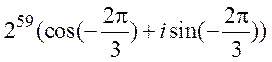 .
.
В алгебраической форме: ![]() =
=![]() ,
,
в показательной форме: ![]() =
=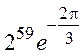 .
.
Задача 1.2. Вычислить ![]() .
.
Решение. Представим
комплексное число ![]() в тригонометрической форме:
в тригонометрической форме:
![]() =
=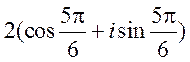 . Воспользуемся следующей формулой
извлечения корня из комплексного числа :
. Воспользуемся следующей формулой
извлечения корня из комплексного числа : 
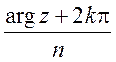 ), где
), где![]() =0,1,2,…,
=0,1,2,…,![]() .
.
Т.е. корень ![]() -ой
степени из комплексного числа принимает ровно
-ой
степени из комплексного числа принимает ровно ![]() значений.
Точки комплексной плоскости, соответствующие значениям
значений.
Точки комплексной плоскости, соответствующие значениям ![]() ,
являются вершинами правильного многоугольника, вписанного в окружность радиуса
,
являются вершинами правильного многоугольника, вписанного в окружность радиуса ![]() с центром в начале координат.
с центром в начале координат.
В данном примере получаем: ![]() =
=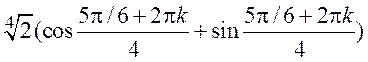 , где
, где ![]() . Тогда корни принимают значения:
. Тогда корни принимают значения:
![]() =
=![]() (
(![]()
![]() +
+![]()
![]()
![]() ),
),
![]() =
=![]() (
(![]()
![]() +
+![]()
![]()
![]() ),
),
![]() =
=![]() (
(![]()
![]() +
+![]()
![]()
![]() ),
),
![]() =
=![]() (
(![]()
![]() +
+![]()
![]()
![]() ).
).
Для построения этих комплексных
чисел на комплексной плоскости ![]() проведем окружность
радиуса
проведем окружность
радиуса ![]() . На окружности отметим точку
. На окружности отметим точку ![]() =
=![]() (
(![]()
![]() +
+![]()
![]()
![]() ), далее, разбивая окружность на четыре
равные части , изобразим остальные точки
), далее, разбивая окружность на четыре
равные части , изобразим остальные точки ![]() ,
,![]() ,
, ![]() . Заметим,
что
. Заметим,
что ![]() радиан соответствуют примерно
радиан соответствуют примерно![]() .
.
Задача 2. Найти произведение
матриц ![]() , где
, где 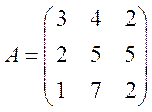 и
и 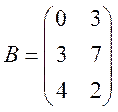 .
.
Решение. ![]() =
=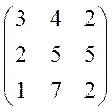
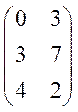 =
=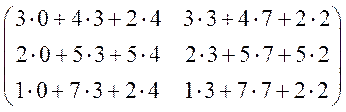 =
=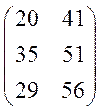
Задача 3. Найти матрицу,
обратную данной. Сделать проверку. 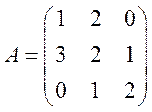 .
.
Решение. Находим
определитель матрицы ![]() .
.
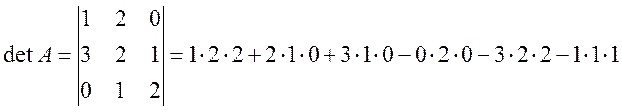 =
=![]() , т.е. данная матрица является неособенной,
обратная матрица существует. Вычислим соответствующие алгебраические дополнения
, т.е. данная матрица является неособенной,
обратная матрица существует. Вычислим соответствующие алгебраические дополнения
![]() :
:
![]() =
=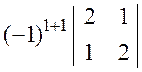 =
=![]() ;
; ![]() =
=![]()
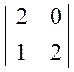 =
=![]() ;
; ![]()
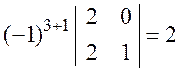 ;
;
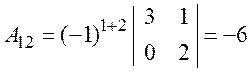 ;
;
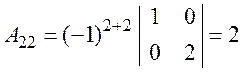 ;
; 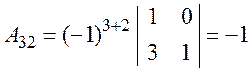 ;
;
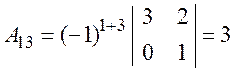 ;
;
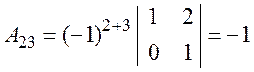 ;
; 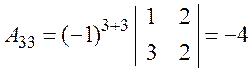 .
.
Находим обратную матрицу ![]() :
:
![]() =
=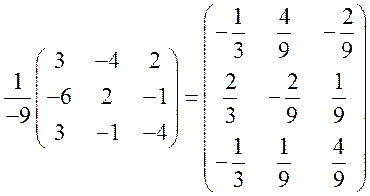 . Проверка заключается в перемножении
матриц
. Проверка заключается в перемножении
матриц
![]() (единичная
матрица). Последнюю операцию выполнять аналогично примеру 2.
(единичная
матрица). Последнюю операцию выполнять аналогично примеру 2.
Задача 4. Решить систему
линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы: 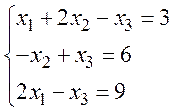 .
.
Решение. Найдем обратную
матрицу![]() к матрице системы
к матрице системы 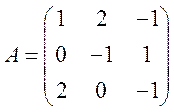 .
.
Аналогично примеру 3 получаем ![]() =
=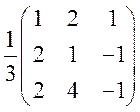
Вектор – столбец решений находится
по формуле: 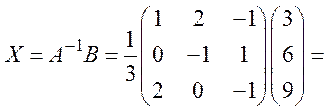
=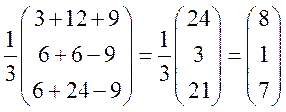 , или
, или
![]() Проверка осуществляется непосредственной
подстановкой найденных значений неизвестных в исходную СЛАУ.
Проверка осуществляется непосредственной
подстановкой найденных значений неизвестных в исходную СЛАУ.
Задача 5. Найти ранг матрицы
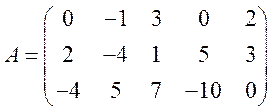 .
.
Решение. Последовательно осуществляем линейные преобразования строк данной матрицы для приведения ее к ступенчатому виду.
Шаг 1. Переставим в данной матрице первую и вторую строки.
Шаг 2. Умножим первый столбец на 1/2,
четвертый столбец умножим на 1/5. В результате получим: 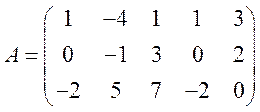 .
.
Шаг 3. Умножим на 2 первую строку и
прибавим её к третьей («заработаем» нуль на месте «3-1»,т.е. вместо (–2)
получим (0)). В результате получим: 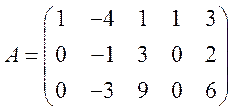 .
.
Шаг 4. Умножим на –3 вторую строку
и прибавим её к третьей («заработаем» нуль на месте «3-2»,т.е. вместо (–3)
получим (0)). Получим: 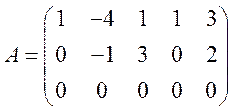
Таким образом, получили ступенчатую
матрицу эквивалентную данной, в которой две ненулевые строки, значит ее ранг
равен 2: ![]() .
.
Задача 6. Решить систему
методом Гаусса: 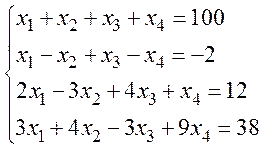 .
.
Решение. Запишем расширенную матрицу СЛАУ:
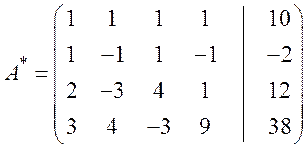 .
.
С помощью эквивалентных преобразований приведём матрицу к верхнетреугольному виду (прямой ход метода Гаусса).
Шаг1. Вычтем из второй строки первую, результат умножим на (–1/2):
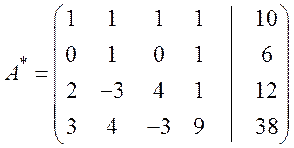
Шаг 2. Вычитаем из третьей строки первую, умноженную на 2:
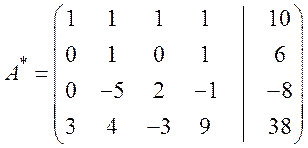
Шаг 3. Вычитаем из четвёртой строки первую, умноженную на 3:
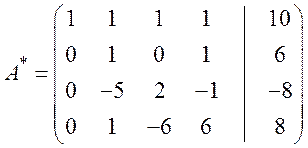
Шаг 4. Прибавляем к третьей строке вторую, умноженную на 5, результат делим на 2:
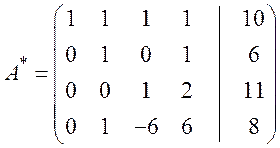
Шаг 5. Вычитаем из четвёртой строки вторую:
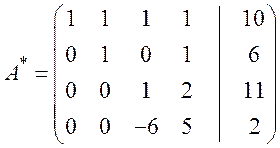
Шаг 6. Прибавляем к четвёртой строке третью, умноженную на 6, результат делим на 17:
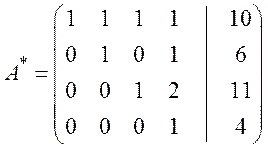
Теперь с помощью эквивалентных преобразований приведём матрицу к диагональному виду (обратный ход метода Гаусса).
Шаги 7, 8, 9. От третьей строки отнимаем четвёртую, умноженную на 2; от второй строки отнимаем четвёртую; от первой строки отнимаем четвёртую.
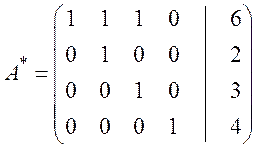
Шаги 10, 11. От первой строки отнимаем третью; от первой строки отнимаем вторую.
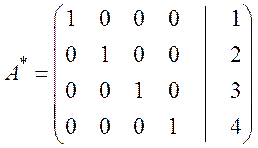
Теперь в последнем столбце получились искомые значения переменных, т.е.
![]()
Задача 7. Найти размерность
и базис подпространства решений однородной системы линейных алгебраических
уравнений (ОСЛАУ). 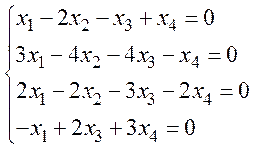 .
.
Решение. Применим прямой ход метода Гаусса (приведем систему уравнений к верхнетреугольному виду). Поступая аналогично примеру 6 вычтем из второй строки первую, умноженную на 3; вычтем из третьей строки первую, умноженную на 2; прибавим первую строку к четвёртой; получим:
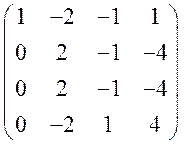 ,
,
последние три строки оказались одинаковыми, значит, матрицу можно привести к следующему виду:
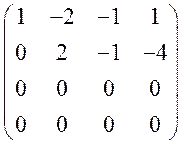 .
.
В качестве базисных переменных
можно взять ![]() , свободные –
, свободные – ![]() .
.
Ранг матрицы равен 2, т.е. ![]() , следовательно, размерность
подпространства решений тоже равна 2.
, следовательно, размерность
подпространства решений тоже равна 2.
Формируем фундаментальную систему
решений (ФСР). Пусть переменные ![]() принимают значения 1, 0
соответственно. Тогда из второго уравнения находим значение
принимают значения 1, 0
соответственно. Тогда из второго уравнения находим значение ![]() из первого уравнения находим значение
из первого уравнения находим значение ![]() Тогда
Тогда 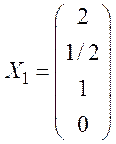 .
.
Пусть теперь переменные ![]() принимают значения 0, 1 соответственно.
Тогда, поступая аналогично, получим
принимают значения 0, 1 соответственно.
Тогда, поступая аналогично, получим ![]()
![]() Откуда
Откуда
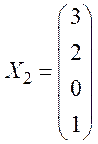 .
. ![]() - образуют
ФСР, общее решение данной однородной СЛАУ имеет вид
- образуют
ФСР, общее решение данной однородной СЛАУ имеет вид ![]() .
.
Задача 8. Доказать, что
векторы ![]() образуют базис и разложить вектор
образуют базис и разложить вектор ![]() по этому базису.
по этому базису.
Решение. Ненулевые векторы ![]() образуют базис тогда и только тогда, когда
они некомпланарны (т.е. не лежат в одной плоскости), значит их смешанное
произведение не должно быть равно 0:
образуют базис тогда и только тогда, когда
они некомпланарны (т.е. не лежат в одной плоскости), значит их смешанное
произведение не должно быть равно 0:
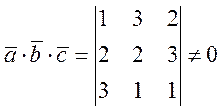 , 121
+ 333 + 221 – 223 – 231 – 131 = 12 ≠ 0. Векторы образуют базис.
, 121
+ 333 + 221 – 223 – 231 – 131 = 12 ≠ 0. Векторы образуют базис.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.