Плазма как сплошная среда. Двухтемпературная плазма

Лекция 4

Плазма как сплошная среда

          Для приближенного описания плазмы с успехом используются модели, рассматривающие плазму как сплошную среду. Наука, изучающая движение проводящих жидкостей и газов посредством совместного решения уравнений гидродинамики и электродинамики, называется магнитной гидродинамикой.

          Феноменологически уравнения движения сплошной среды можно получить из законов сохранения массы, количества движения и энергии:

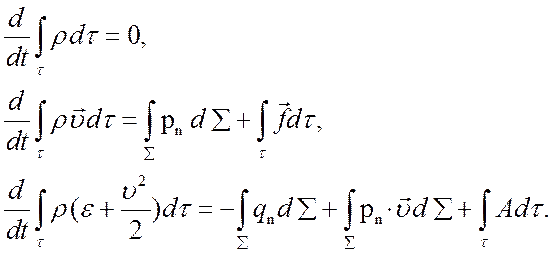                                          (4.1)

Здесь  - скорость сплошной среды, равная скорости центра инерции частиц, находящихся в объеме  в окрестности рассматриваемой точки;  - «жидкий» объем ограниченный поверхностью ;  - плотность среды;  - плотность поверхностных сил;  - плотность внешних объемных сил;  - внутренняя энергия единицы массы;  - поток тепла через поверхность ;     -  удельная (на единицу объема) работа внешних сил.     В качестве объемных сил в дальнейшем будем рассматривать только силы воздействия электромагнитного поля на среду

          ,                                                                                    (4.2)

где  - плотность заряда,  - плотность тока,  - напряженность электрического поля,  - индукция  магнитного поля. Тогда  есть работа электромагнитного поля

          .                                                                                               (4.3)

          В механике сплошных сред доказывается, что плотность поверхностных сил  задается тензором напряжений

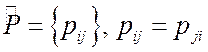          .                                                                                 (4.4)

Для двухпараметрических сред

          ,                                                                                    (4.5)

где  - давление,  - дельта функция

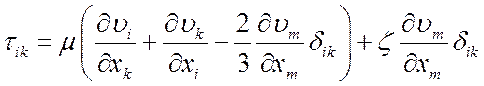                                                    (4.6)

тензор вязких напряжений,  - первый и второй коэффициенты вязкости.

          Поток тепла есть

          ,                                                                                    (4.7)

где Т - температура,  - коэффициент теплопроводности,  - радиационный поток.

          Используя формулу Остоградского-Гаусса 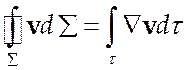, из интегральных уравнений (4.1) можно получить дифференциальные уравнения движения:

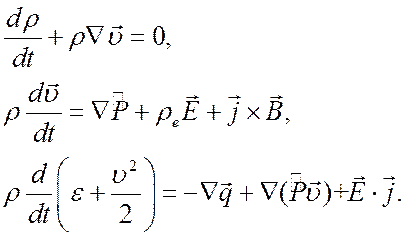                                                              (4.8)

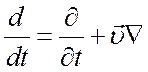 - субстанциональная производная. При получении первого уравнения использовано равенство 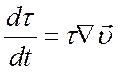, а при выводе остальных - равенство .

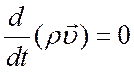К системе уравнений (4.8) необходимо добавить систему замыкающих уравнений:

Уравнение состояния

.                                                                                           (4.9)

Систему уравнений Максвелла

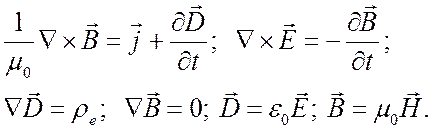                                                 (4.10)

Закон Ома, связывающий плотность тока с напряженностью электромагнитного поля и параметрами среды

          .                                                                                  (4.11)

Систему уравнений, определяющих радиационный поток тепла

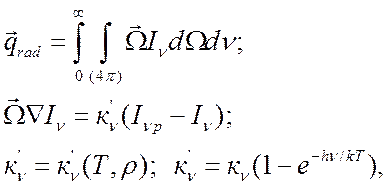                                                        (4.12)

где - спектральная интенсивность излучения,  - спектральная интенсивность равновесного излучения,  - единичный вектор телесного угла в направлении движения квантов,  - спектральный коэффициент поглощения.

На практике в разных задачах используются другие формы записи уравнения энергии, которые получаются из последнего уравнения (4.8) при помощи термодинамических соотношений и первых двух уравнений (4.8). Умножим уравнение импульсов на  скалярно 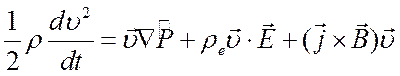 и подставим в уравнение энергии. С учетом (4.5) в результате получим

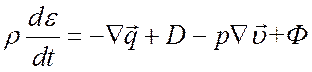,                                                                 (4.13)

где

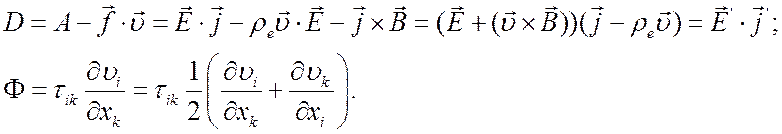
 - называется джоулевым теплом,  - называется диссипативной функцией (связана с выделением тепла за счет вязкого трения).

          Для двухпараметрических сред

,

где  - удельный объем,  - энтропия одного грамма среды, то уравнение (4.13) можно записать в виде

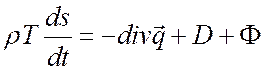          .                                                                        (4.14)

Двухтемпературная плазма

          Во многих случаях температура электронного газа  отличается от температуры тяжелых частиц . Как правило, это имеет место для не очень плотной плазмы при наличии сильных внешних электромагнитных полей, когда электрон на средней длине свободного пробега получает энергию, значительно превосходящую тепловую энергию газа. Удельная же электропроводность и другие коэффициенты в уравнениях движения зависят от  . Поэтому в таких случаях необходимо включать  в число переменных, характеризующих состояние газа, и рассматривать еще одно уравнение, определяющее температуру электронов. Выведем это уравнение эвристически, рассматривая газ как сплошную среду.

          Каждую компоненту газовой смеси можно представить себе как отдельную среду, сосуществующую с другими компонентами. Каждая однокомпонентная среда описывается системой уравнений, выражающих законы сохранения для сплошных сред (3.8), но содержащих добавочные члены, которые описывают взаимодействие между однокомпонентными средами.

          Чтобы составить уравнение, выражающее закон сохранения энергии для электронного газа воспользуемся первым началом термодинамики

          ,                                                                       (4.15)