Влияние столкновений - холловский ток и проскальзывание ионов
В промежутках между
столкновениями отдельные частицы дрейфуют со скоростью пропорциональной ![]() . Диффузионные скорости ─ это
макроскопические характеристики такого движения. Рассмотрим качественно влияние
магнитного поля В на диффузионные скорости заряженных частиц. Будем
рассматривать плазму в системе отсчета, движущейся со средней массовой
скоростью газа.
. Диффузионные скорости ─ это
макроскопические характеристики такого движения. Рассмотрим качественно влияние
магнитного поля В на диффузионные скорости заряженных частиц. Будем
рассматривать плазму в системе отсчета, движущейся со средней массовой
скоростью газа.
Электрическое поле в
этой системе отсчета равно ![]() , а магнитная индукция
, а магнитная индукция ![]() . В предыдущей лекции было показано, что
магнитное поле В не оказывает никакого влияния на компоненту скорости
частиц в направлении вектора
. В предыдущей лекции было показано, что
магнитное поле В не оказывает никакого влияния на компоненту скорости
частиц в направлении вектора ![]() . Следовательно, эта
компонента определяется только величиной
. Следовательно, эта
компонента определяется только величиной ![]() ,
которую для простоты примем равной нулю.
,
которую для простоты примем равной нулю.
Рассмотрим плазму,
находящуюся в однородных и постоянных полях ![]() и
и ![]() . Если бы поля В не было, электроны
и ионы двигались бы в поле
. Если бы поля В не было, электроны
и ионы двигались бы в поле ![]() с разными, но
постоянными средними скоростями в направлении оси y,
так что отличной от нуля была бы лишь компонента тока
с разными, но
постоянными средними скоростями в направлении оси y,
так что отличной от нуля была бы лишь компонента тока ![]() .
При наличии магнитного поля ситуация зависит от того, в какой степени
прямолинейные участки ломаной линии траектории заряженных частиц искривятся под
действием поля В.
.
При наличии магнитного поля ситуация зависит от того, в какой степени
прямолинейные участки ломаной линии траектории заряженных частиц искривятся под
действием поля В.
Число оборотов,
делаемых частицей за время между двумя столкновениями, приближенно дается
параметром Холла ![]() . В случае когда величина
. В случае когда величина ![]() мала и для электронов, и для ионов,
влиянием магнитного поля В также мало и им можно пренебречь.
мала и для электронов, и для ионов,
влиянием магнитного поля В также мало и им можно пренебречь.
При равных температурах электронов и ионов имеем
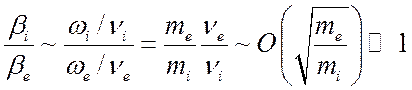 .
(4.31)
.
(4.31)
Таким образом, в случае сильно столкновительной
плазмы, когда ![]() , (
, (![]() согласно
(4.31)) влиянием магнитного поля В можно пренебречь.
согласно
(4.31)) влиянием магнитного поля В можно пренебречь.
В другом крайне случае
─ в случае бесстолкновительной плазмы, т.е. при ![]() ,
электроны и ионы в среднем делают много оборотов между двумя столкновениями.
Поэтому усредненное движение и электронов и ионов представляет собой дрейф со
скоростью
,
электроны и ионы в среднем делают много оборотов между двумя столкновениями.
Поэтому усредненное движение и электронов и ионов представляет собой дрейф со
скоростью 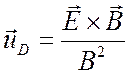 . Отсюда следует, что в этом предельном
случае
. Отсюда следует, что в этом предельном
случае ![]() .
.
Неравенству (4.31) удовлетворяет промежуточный случай, когда
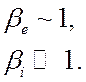 (4.32)
(4.32)
 То есть, когда ионный газ ─
сильно столкновительный, а электронный нет. Направление средней диффузионной
скорости ионов по-прежнему будет совпадать с осью у, но из-за дрейфа со
скоростью
То есть, когда ионный газ ─
сильно столкновительный, а электронный нет. Направление средней диффузионной
скорости ионов по-прежнему будет совпадать с осью у, но из-за дрейфа со
скоростью ![]() у средней диффузионной скорости электронов
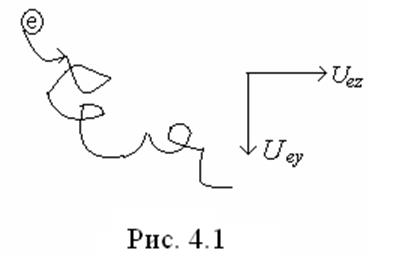
появится компонента в направлении оси х. Поскольку движение прерывается
столкновениями (рис. 4.1), фактическая скорость будет составлять только часть
дрейфовой скорости
у средней диффузионной скорости электронов
появится компонента в направлении оси х. Поскольку движение прерывается
столкновениями (рис. 4.1), фактическая скорость будет составлять только часть
дрейфовой скорости ![]() . При достаточно больших
. При достаточно больших ![]() можно получить следующий приближенный
результат:
можно получить следующий приближенный
результат:
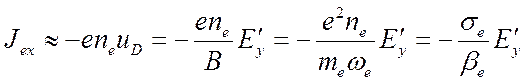 , (4.33)
, (4.33)
 где
где 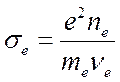 ─
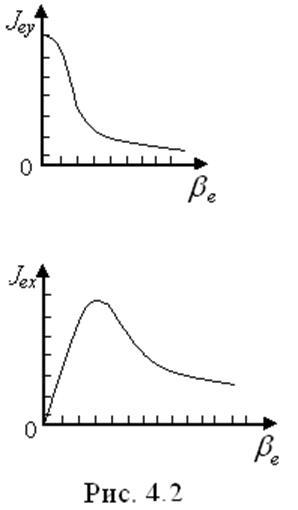
электронная проводимость плазмы. Качественная зависимость компонентов плотности
тока от параметра Холла представлена на рис. (4.2). Компонента тока
─
электронная проводимость плазмы. Качественная зависимость компонентов плотности
тока от параметра Холла представлена на рис. (4.2). Компонента тока ![]() в направлении перпендикулярном
электрическому полю и полю магнитной индукции, называется холловским током.
в направлении перпендикулярном
электрическому полю и полю магнитной индукции, называется холловским током.
Неравенство (4.31) выполняется также во втором промежуточном случае, когда
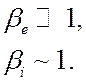 (4.34)
(4.34)
т.е., когда электронный газ почти
бесстолкновительный, а ионный нет. При таких условиях ионный ток ![]() может давать основной вклад в у-компоненту
полного тока, поскольку
может давать основной вклад в у-компоненту
полного тока, поскольку ![]() . Это явление получило
название проскальзыванием ионов. Проскальзывание ионов возможно только в
частично ионизованных газах; в случае же полностью ионизованного газа в силу
общего требования равенства нулю суммы всех диффузионных потоков (формула
(3.19)), величина
. Это явление получило
название проскальзыванием ионов. Проскальзывание ионов возможно только в
частично ионизованных газах; в случае же полностью ионизованного газа в силу
общего требования равенства нулю суммы всех диффузионных потоков (формула
(3.19)), величина 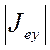 всегда должна быть больше
всегда должна быть больше ![]() независимо от механизмов, вызывающих
движение.
независимо от механизмов, вызывающих
движение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.