Плазма как сплошная среда. Двухтемпературная плазма, страница 2

где  ─ внутренняя энергия на единицу массы,  ─ масса газа в объеме ,  ─ удельный  объем,  ─ удельная (на единицу массы) мощность тепловых источников, и уравнением неразрывности

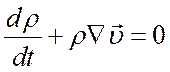          .                                                                                      (4.16)

Поскольку при любых химических превращениях  масса газа сохраняется  уравнение (4.15) можно записать как

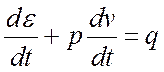          .                                                                                       (4.17)

Проведем ряд простейших преобразований уравнения (4.17):

                                                

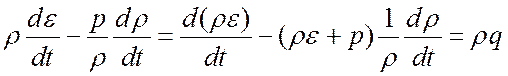
Откуда с учетом выражения (4.16) окончательно будем иметь

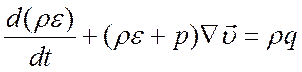          .                                                                   (4.18)

Здесь  ─ суммарная мощность тепловых источников (стоков) в единице объема.

          Для электронов имеем , , 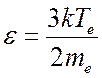 и уравнение (4.18) запишется в виде

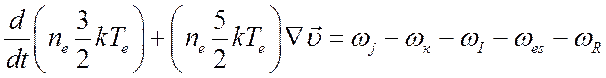.                       (4.19)

Правая часть уравнения (4.19) содержит все виды источников (стоков) энергии (удельные мощности):

 - подвод энергии за счет электромагнитного поля (Джоулев нагрев),  

 - потери энергии за счет теплопроводности, где  - коэффициент электронной теплопроводности;

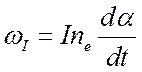 - потери энергии на ионизацию, где  - потенциал ионизации,  - степень ионизации;

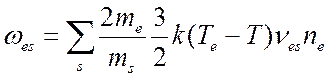 - потери энергии за счет упругих столкновений электронов с тяжелыми частицами сорта  (см. формулу (3.51)), где  - частота столкновений между электроном и тяжелыми частицами;

 - радиационные потери энергии, связанные с тормозным и рекомбинационным излучением. Здесь 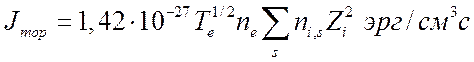,  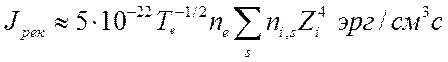─ лучеиспускательные способности тормозного излучения [1] и рекомбинационного излучения [2] соответственно. Суммирование распространяется на все разновидности ионов.

          В рассматриваемом приближении взаимодействие электронного газа со средой учитывается введением в правую часть уравнения энергии  обменного члена  со знаком плюс и удалением членов, вошедших  теперь в уравнение энергии для электронов (энергии ионизации из выражения для свободной энергии, электронной теплопроводности из общего потока тепла, джоулевого нагрева, тормозного и рекомбинационного излучения из лучистого потока).

Частично ионизованный газ: уравнения движения трехкомпонентной среды

          Пусть в единице объема содержится  нейтральных частиц,  ионов и  электронов. Для простоты будем считать, что зарядовое число ионов , тогда плотность объемного заряда равна . Далее будем считать

          .                                                                                        (4.20)

Определим степень ионизации как отношение числа ионизованных атомов к начальному числу атомов

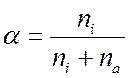          .                                                                                            (4.21)

Плазму будем рассматривать как совокупность трех сред: электронной, ионной  и нейтральной, - движущихся друг сквозь друга. Взаимодействие между компонентами происходит в результате столкновений и сводится к  некоторой усредненной объемной силе, равной среднему изменению импульса при столкновении частиц, принадлежащих разным компонентам. Электронный, ионный и нейтральный газы считаются идеальными и суммарное давление равно сумме парциальных давлений каждой из компонент

          .                                                                                    (4.22)

Вследствие пропорциональности давления  числу частиц имеем:

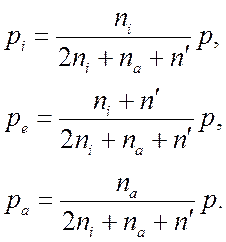                                                                                         (4.23)