Плазма как сплошная среда. Двухтемпературная плазма, страница 3

          В пространстве, занятом движущейся средой, задано электрическое поле  и магнитное поле . При этом предполагается, что  и  определяются как внешними полями, так и зарядами и токами в самой среде.

          Уравнение движения, соответствующее  компоненте  может быть записано в виде

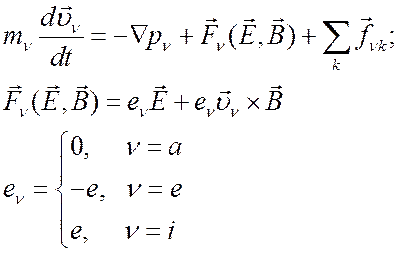                                                      (4.24)

Здесь  есть объемная электромагнитная сила , а  ─ сила, действующую на единицу объема - й компоненты со стороны частиц -той компоненты.

          Определим силу, действующую на каждую из компонент, возникающую за счет столкновений частиц этой компоненты с частицами другой компоненты, следующим образом:

                                                                           (4.25)

где  ─ число частиц -го сорта в единице объема,  ─ среднее время между столкновениями частиц -го сорта с частицами - го сорта, за которое частица -го сорта теряет в среднем импульс . Обычно в качестве  выбирается величина

         

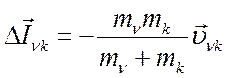
( ─ средняя скорость частиц -й компоненты относительно -й компоненты), которая соответствует средней потере импульса при  упругом столкновении двух частиц , движущихся с относительной скоростью  в предположении изотропности рассеяния. Согласно неравенству (4.20), для электронного газа

         

а для ионного и нейтрального газов

         

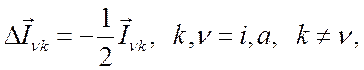
где  ─ импульс частиц  -го газа относительно частиц - го газа.

          Теперь легко написать уравнение движения для каждой из компонент среды. Пусть  ─ скорость движения всей среды,  ─ скорость движения ионного относительно среды,  ─ скорость движения электронного относительно ионного газа. Скорость движения нейтрального газа определяется через скорость среды и скорости ионного газа и  электронного газа по формуле

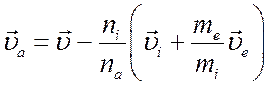          .                                                                        (4.26)

При выводе этого соотношения считается, что скорость элемента среды совпадает со скоростью его центра масс, и используется неравенство (4.20). Последний член оставлен, несмотря на малую массу электрона, в связи с тем, что может оказаться . Коме того. Здесь и всюду в дальнейшем считается, что

          .                                                                                                   (4.27)

Так как значительные концентрации объемного заряда не могут возникнуть при отсутствии специальных внешних условий. В связи с этим членами 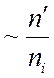 всюду пренебрегаем по отношению к членам ~1. Условие (4.27) не равносильно предположению об отсутствии пространственного заряда, т.к. малое превышение числа электронов над числом ионов может дать заметный вклад в силу, действующую на среду со стороны электрического поля  и в плотность тока за счет переноса зарядов вместе со средой.

          Так как средний импульс электронов относительно ионов равен , а относительно нейтральных частиц

          ,

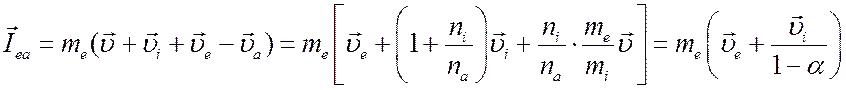то уравнение движения электронного газа можно записать в виде

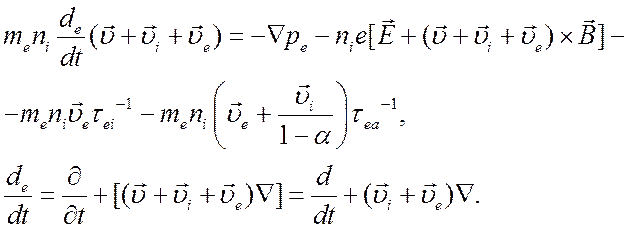                    (4.28)

Импульс ионов относительно нейтральных частиц равен

         

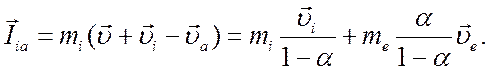
Используя это выражение, запишем уравнение движения ионного газа

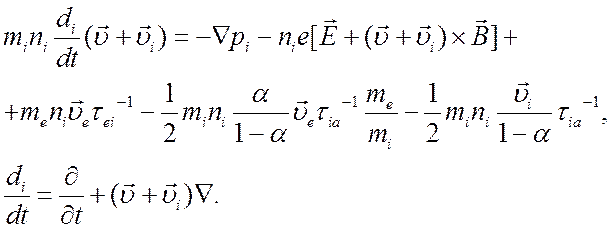                                  (4.29)

В уравнениях  (4.28) и (4.29)  - соответственно время между столкновениями электронов с ионами, ионов с нейтральными частицами и электронов с нейтральными частицами. Вместо уравнения движения нейтрального газа будем пользоваться уравнением смеси в целом, которое является следствием уравнения движения нейтрального газа и уравнений (4.28), (4.29), (4.20) и (4.22):

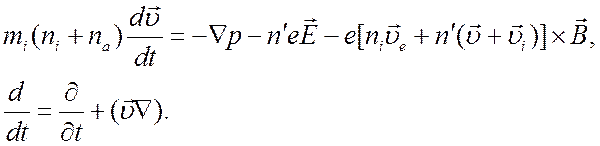                                    (4.30)

Здесь мы воспользовались определением плотности тока

         

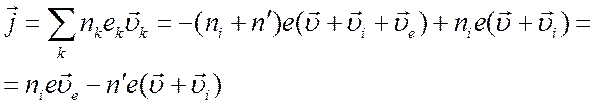
и неравенством (4.27).