|
Задание для контрольной работы по теоретической механике (кинематика К3) |
|
|
|
a) Механизм состоит из ступенчатых колес 1,2,3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на ступень колеса 3. Радиусы ступеней колес равны соответственно r1=2см, R1=4см, r2=6см, R2=8см, r3=12см, R3=16см. На ободьях колес расположены точки А и С. Ведущим звеном механизма является рейка 4, ее закон движения – s4=4(7t-t2). Определить в момент времени t=2с скорости vA, vC и ускорения e2, aA, a5. b) По заданному уравнению прямолинейного поступательного движения груза 1 ( x = 4+90t2, x измеряется в см, t – в секундах ) определить скорость, а также тангенциальное, центростремительное и полное ускорение точки М механизма в момент времени, когда путь, пройденный грузом, равен 0.5м. Данные для расчета: R2=20см, r2=10см, R3=30см, r3=10см. |
Решение задачи a
|
|
Условимся обозначать скорости точек, лежащих на внешних ступенях колес через v, точек, лежащих на внутренних ступенях – через u. 1. Определяем сначала угловые скорости всех колес как функцию времени t. Зная закон движения рейки 4, находим ее скорость:
Так как рейка и колесо 2 находятся в зацеплении, то v2=v4 или w2R2=v4. Отсюда |
Скорость движения ремня u2=u1=w2r2=w1r1, тогда
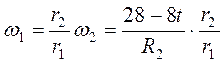
Колеса 1 и 3 находятся во внешнем зацеплении, поэтому v1=w1R1=v3=w3R3 и
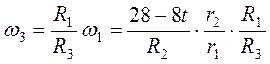
2. Определяем vA. Так как
vA=w1R1, то 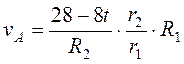 и при t=2с после подстановки всех численных значений получим vA=18 см/с
и при t=2с после подстановки всех численных значений получим vA=18 см/с
3. Определяем vС. Так как точка С лежит на ободе ступени колеса 3, радиус которой – r3, то vC=u3=w3r3. Подставив сюда численные значения будем иметь:
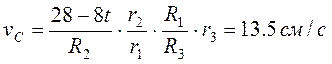
4. Определяем угловое ускорение e2. Получим его просто продифференцировав по времени зависимость w2 от t и подставив численные значения:
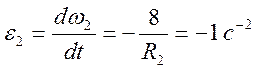
На рисунке дуговые стрелки угловых скоростей колес направлены противоположно дуговым стрелкам угловых ускорений. Это означает, что в рассматриваемый момент времени (t=2с) колеса механизма замедляют свое вращение (в частности, e2 имеет отрицательное значение).
5. Для определения aA (ускорение точки A) примем во внимание, что
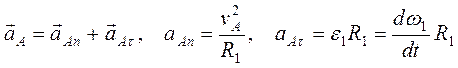 .
.
Нормальное (центростремительное) ускорение точки А численно равно aAn = 81 см/с2, тангенциальное (касательное) ускорение aAt= -12 см/с2. Отрицательное значение показывает, что вектор aAt направлен противоположно вектору скорости vA, вектор нормального ускорения направлен к центру колеса 1.
Полное ускорение точки А, таким образом, равно:
![]() 81.88 см/с2.
81.88 см/с2.
6. Определяем a5. Ускорение a5 груза 5 равно тангенциальному ускорению точки С aCt:
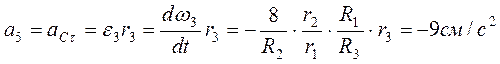
Решение задачи b
|
|
Условимся обозначать скорости точек, лежащих на внешних ступенях колес через v, точек, лежащих на внутренних ступенях – через u. 1. Определяем сначала угловые скорости и ускорения всех колес как функцию времени t. Зная закон движения груза 1, находим его скорость:
Так как нить намотана на внешнюю ступень колеса 2, то v1=v2 или v1=w2R2. Отсюда |
Внешняя ступень колеса 3 находится в зацеплении с внутренней ступенью колеса 2, скорости точек этих ступеней равны : v3=u2 или w3R3=w2r2. Получаем
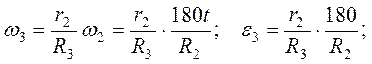
Угловые скорости и ускорения имеют одинаковые знаки, поэтому их дуговые стрелки изображены на рисунке направленными в одинаковые стороны.
2. Определяем время, за которое груз 1 пройдет заданный путь:
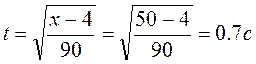
3. Определяем скорость vM. Точка М находится на ободе ступени радиуса r3, ее скорость равна u3 = vM = w3r3. Для t=0.7с вычисляем скорость точки: vM = 2.1см/с. Скорость точки направлена по касательной к ободу ступени колеса 3.
4. Определяем тангенциальное ускорение at точки М. Для него имеем:
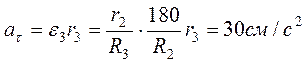
Это ускорение направлено по касательной к ободу ступени колеса 3, также, как и скорость vM.
5. Определяем центростремительное ускорение an точки М. Это ускорение определяется по формуле 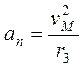 , что дает нам значение an=0.441
см/с2. Центростремительное ускорение всегда направлено к оси
вращения.
, что дает нам значение an=0.441
см/с2. Центростремительное ускорение всегда направлено к оси
вращения.
6. Полное ускорение точки М получим по формуле : ![]() , это даст нам значение a=30.003
см/с2, то есть полное ускорение почти полностью определяется своей
тангенциальной компонентой.
, это даст нам значение a=30.003
см/с2, то есть полное ускорение почти полностью определяется своей
тангенциальной компонентой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.