Лекция 8.
Гироскопом называется быстро вращающееся твердое тело, ось
которого может менять направление в пространстве. Симметричный гироскоп –
обладающий симметрией относительно некоторой оси – геометрической оси. Обычно
одна из точек оси фигуры гироскопа закреплена. Эту закрепленную точку называют
точкой опоры гироскопа. В общем смысле точкой опоры гироскопа называют такую т.
![]() относительно которой рассматривается
вращение гироскопа. В наиболее общем случае движение гироскопа складывается из
вращения относительно оси, проходящей через мгновенную ось и движения точки
опоры. Простой иллюстрацией движения гироскопа является движение быстро
раскрученного детского волчка
относительно которой рассматривается
вращение гироскопа. В наиболее общем случае движение гироскопа складывается из
вращения относительно оси, проходящей через мгновенную ось и движения точки
опоры. Простой иллюстрацией движения гироскопа является движение быстро
раскрученного детского волчка
Будем в дальнейшем рассматривать уравновешенный гироскоп,
состоящий из двух маховиков для простоты одинаковых, жестко насаженных на общую
ось. Один из маховиков выполняет роль противовеса. Пусть ось гироскопа
подвешена в некоторой точке ![]() . Гироскоп способен без
трения вращаться как относительно оси симметрии, так и относительно
вертикальной оси (см. рис. n1). Движение гироскопа под
действием внешних сил называется прецессией.
. Гироскоп способен без
трения вращаться как относительно оси симметрии, так и относительно
вертикальной оси (см. рис. n1). Движение гироскопа под
действием внешних сил называется прецессией.
Если маховики не вращаются, то приложение внешней силы в
какой либо точке оси, очевидно, приведет к смещению оси в направлении
приложенной силы. Оказывается, если маховики быстро раскручены, то приложение
внешней силы в прежней точке оси приводит к смещению вовсе не в направлении
этой силы! В самом деле, будем считать, что гироскоп вращается с угловой
скоростью ![]() относительно оси симметрии и, как правило,
с угловой скоростью
относительно оси симметрии и, как правило,
с угловой скоростью ![]() относительно вертикальной. В
реальных гироскопах
относительно вертикальной. В
реальных гироскопах ![]() . Вследствие этого
. Вследствие этого ![]() . Пусть внешняя сила приложена к оси
гороскопа вертикально вниз. Эта внешняя сила создает момент относительно точки
подвеса
. Пусть внешняя сила приложена к оси
гороскопа вертикально вниз. Эта внешняя сила создает момент относительно точки
подвеса ![]() , направленный горизонтально в плоскость
чертежа -
, направленный горизонтально в плоскость
чертежа - ![]() . Согласно основному уравнению динамики
твердого тела
. Согласно основному уравнению динамики
твердого тела ![]() получаем, что изменение момента
импульса также будет направлено по горизонтали, иначе говоря
получаем, что изменение момента
импульса также будет направлено по горизонтали, иначе говоря ![]() . В этом случае модуль момента импульса не
меняется, меняется только его направление в пространстве. Нетрудно усмотреть в
этом выводе аналогию с вращательным движением точки, в которм ускорение
перпендикулярно скорости
. В этом случае модуль момента импульса не
меняется, меняется только его направление в пространстве. Нетрудно усмотреть в
этом выводе аналогию с вращательным движением точки, в которм ускорение
перпендикулярно скорости ![]() . Следовательно вектор
. Следовательно вектор ![]() совершает медленное вращение относительно
вертикальной оси – говорят, что прецессирует.
совершает медленное вращение относительно
вертикальной оси – говорят, что прецессирует.
Пусть ![]() угловая скорость
прецессии. Тогда
угловая скорость
прецессии. Тогда ![]() , (для сравнения
, (для сравнения ![]() ). Т.к.
). Т.к. ![]() , то
, то ![]() . Из этого соотношения можно определить
угловую скорость прецессии:
. Из этого соотношения можно определить
угловую скорость прецессии:
![]() (1)
(1)
Пример. Прецессия волчка. Волчок – быстро раскрученное
симметричное относительно оси тело. (см. рис. n3).
Рассмотрим регулярную прецессию оси волчка вокруг вертикальной оси. Ось волка
отклонена на угол ![]() относительно вертикали и
вращается с малой угловой скоростью
относительно вертикали и
вращается с малой угловой скоростью ![]() . Момент импульса волчка
вследствие быстрого вращения относительно геометрической оси
. Момент импульса волчка
вследствие быстрого вращения относительно геометрической оси ![]() . За достаточно малый интервал времени -
. За достаточно малый интервал времени - ![]() , где
, где ![]() - угол
в горизонтальной плоскости. Из уравнения динамики:
- угол
в горизонтальной плоскости. Из уравнения динамики: 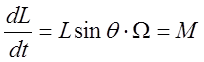 , где
, где ![]() - момент силы тяжести относительно точки
опоры.
- момент силы тяжести относительно точки
опоры. ![]() . Сравнивая, имеем:
. Сравнивая, имеем:
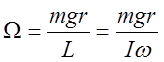 ,
, ![]() -
расстояние центра масс волчка от точки опоры.
-
расстояние центра масс волчка от точки опоры.
Неинерциальные системы отсчета.
До сих пор все явления нами рассматривались в инерциальных системах отсчета, в которых справедлив принцип относительности Галилея. Существуют помимо инерциальных неинерциальные системы – движущиеся с ускорением. Рассмотрение каких – либо явлений в таких системах имеет особенности.
Наиболее простой вид неинерциальной системы отсчета – прямолинейно движущаяся с постоянным ускорением система. Физическая реализация такой системы – вагон, двигающийся с постоянным ускорением на прямолинейном отрезке пути.
Рассмотрим материальную точку, подвешенную на
нерастяжимой, невесомой нити длины ![]() к потолку вагона.
Очевидно, что нить отклонится на некоторый угол относительно вертикали. В
лабораторной системе отсчета существуют две силы – сила тяжести
к потолку вагона.
Очевидно, что нить отклонится на некоторый угол относительно вертикали. В
лабораторной системе отсчета существуют две силы – сила тяжести ![]() и сила натяжения нити
и сила натяжения нити ![]() . Под действием этих сил тело приобретает
ускорение
. Под действием этих сил тело приобретает
ускорение ![]() :
: ![]()
![]() . Записывая уравнение движения в проекциях
(см. рис. n6) находим угол отклонения нити:
. Записывая уравнение движения в проекциях
(см. рис. n6) находим угол отклонения нити:
![]() .
.
Перейдем в систему отсчета, связанную с вагоном. Силы
тяжести и натяжения нити по- прежнему есть, однако в этой системе отсчета тело
покоится. Очевидно, что имеется ненулевая сумма сил ![]() , при
этом ускорение, подчеркнем, в системе вагона равно нулю. Возможно два вывода из
этой неоднозначности: либо отказаться от II-го закона
Ньютона в неинерциальной системе, либо изменить его вид, что он был справедлив
в этой системе.
, при
этом ускорение, подчеркнем, в системе вагона равно нулю. Возможно два вывода из
этой неоднозначности: либо отказаться от II-го закона
Ньютона в неинерциальной системе, либо изменить его вид, что он был справедлив
в этой системе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.