Элементарная теория гироскопа. Неинерциальные системы отсчета. Закон Бэра, страница 3

Ответ на этот вопрос состоит в учете обеих фиктивных сил – центробежной и кориолисовой. Вернемся к поставленной задаче (см. рис. n7). Платформа вращается против часовой стрелки, вектор угловой скорости платформы направлен вдоль оси вращения «на нас». В таком случае фиктивная центробежная сила, действующая на произвольное тело, находящееся на расстоянии  от центра и неподвижное в лабораторной системе отсчета  и направлена эта сила вдоль радиуса от центра. Теперь подсчитаем кориолисову силу. Векторное произведение  при указанном направлении векторов направлено к центру, причем . Абсолютное значение силы Кориолиса: . Сумма сил центробежной и кориолисовой направлена к оси вращения и равна , что дает движение с ускорением . Вот почему тела не ускоряются вдоль радиуса. Они движутся по окружностям постоянного радиуса.

Рассмотрим общий случай: помимо поперечной имеется составляющая скорости тела вдоль радиуса. Будем считать скорость тела в лабораторной – инерциальной системе отсчета – постоянна, следовательно, результирующая всех сил, действующих на тело равна нулю. Или, иначе говоря, реальных сил нет.

Будем считать, что в некоторый начальный момент времени имеются составляющие скорости тела в лабораторной системе отсчета в поперечном относительно радиуса направлении , и в продольном относительно радиуса направлении . Равенство позволяет утверждать, что тело имеет нулевую во вращающейся с угловой скоростью системе отсчета скорость. Продольная скорость одинакова в обеих системах отсчета. Через достаточно малый интервал времени  тело сдвигается из начальной точки  в т.(см. рис. n8). Сдвиг составит по радиусу , поперек радиуса . Эти смещения высчитаны в лабораторной системе отсчета. Однако на вращающемся диске т. , полученная после сдвига по радиусу на  вместе с диском переместится в т.  в поперечном направлении на . Следовательно, относительно вращающейся системы отсчета «реальный» сдвиг равен отрезку . Происходит отставание от диска, которое, очевидно, должно объясняться действием силы – силы Кориолиса.  На рис. n9 при указанном направлении векторов кориолисова сила направлена вниз и численно равна . Нетрудно убедиться, что поперечное смещение под действием этой силы при равноускоренном движении:

,

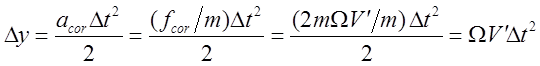что совпадает с полученным ранее значением .

Суммируя все обсуждавшееся ранее, следует записывать выражение для II-го закона Ньютона во вращающейся системе отсчета в виде:

                      (16)

Здесь  - ускорение во вращающейся, неинерциальной системе отсчета, - результирующая реальная сила, - соответственно центробежная и кориолисова фиктивные силы,   - скорость во вращающейся системе отсчета.

Закон Бэра.

В северном полушарии реки, текущие с юга на север имеют разные окружные вместе с Землей линейные скорости. Действительно в низких широтах, вблизи экватора, окружные скорости больше, чем в высоких широтах из-за уменьшения радиуса относительно оси вращения. (см. рис. n10). Посмотрим, как направлена кориолисова сила, действующая на произвольную выделенную массу воды, смещающуюся на север. Считая направление вращения Земли против часовой стрелки, раскрывая векторное произведение находим, что сила Кориолиса направлена с запада на восток. Это приводит к тому, что сила, действующая на поток со стороны правого берега больше, чем со стороны левого. Поэтому правый (восточный) берег реки более подмыт (более обрывист) по сравнению с левым.

Для рек, текущих с севера на юг аналогичные рассуждения приводят к выводу, что более крутым будет западный, правый берег.

Оказывается, что влиянием кориолисовой силы объясняется закручивание циклонов в тропических широтах. Как правило, вследствие более интенсивного нагрева потоки воздуха в северном полушарии движутся к экватору с севера. Движущийся таким образом поток воздуха кориолисова сила отклоняет вправо и, следовательно, закручивает по часовой стрелке. Напротив, в южном полушарии поток отклоняется влево, против часовой стрелки. Строго на экваторе вследствие отсутствия меридиональной составляющей вектора скорости потока воздуха может возникнуть только вертикальная – направленная вдоль радиуса Земли составляющая кориолисовой силы.