|
Задание для контрольной работы по теоретической механике (статика С4) |
|
|
|
a. Найти координаты центра масс каркаса, составленного из тонких однородных стержней одинакового погонного веса и длины l=0.44 м. |
|
|
b. Найти координаты центра масс однородной плоской фигуры, показанной на рисунке. Размеры указаны в метрах. |
|
|
c. Найти координаты центра масс однородной объемной фигуры, показанной на рисунке. Размеры указаны в сантиметрах. |
Решение задачи a)
Для определения положения центра масс каркаса воспользуемся формулами :
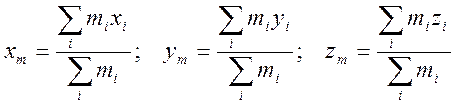 (1)
(1)
В качестве массы будем использовать пропорциональную ей величину – длину элементов (стержней).
Введем систему координат Oxyz соответственно показанному на рисунке.
Координаты центров масс частей каркаса (стержней) в выбранной системе координат и их длины имеют значения:
x1=0 м, y1=0 м, z1=-0.22 м, L1=0.44 м;
x2=-0.44 м, y2=0 м, z2=-0.22 м, L2=0.44 м;
x3=-0.44 м, y3=0.44 м, z3=-0.22 м, L3=0.44 м;
x4=0 м, y4=0.44 м, z4=-0.22 м, L4=0.44 м;
x5=-0.22 м, y5=0 м, z5=0 м, L5=0.44 м;
x6=-0.44 м, y6=0.22 м, z6=0 м, L6=0.44 м;
x7=-0.22 м, y7=0.44 м, z7=0 м, L7=0.44 м;
x8=0 м, y8=0.22 м, z8=0 м, L8=0.44 м;
x9=0 м, y9=0 м, z9=0.22 м, L9=0.44 м;
x10=-0.22 м, y10=0 м, z10=0.44 м, L10=0.44 м;
x11=-0.44 м, y11=0 м, z11=0.22 м, L11=0.44 м;
Подставим полученные значения в формулы (1) и найдем координаты центра масс С каркаса:
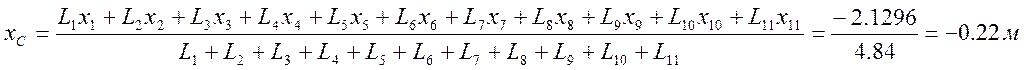
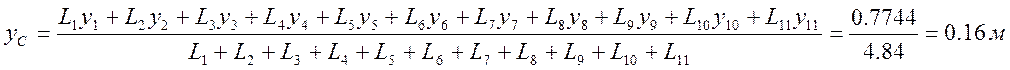
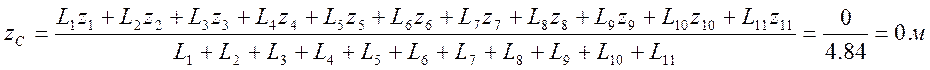
Решение задачи b)
|
|
Для определения положения центра масс плоской фигуры воспользуемся формулами :
В качестве массы будем использовать пропорциональную ей величину – площадь элементов. |
Нашу фигуру можно представить в следующем виде:
Фигура = [1]Квадрат (2х2) + [2]Полудиск (R=1) –[3]диск (d=0.5) –[4]треугольник –[5]полудиск (R=0,4) –
-[6]прямоугольник – [7]сегмент
В формулах считаем, что «вычитаемые» части имеют отрицательную массу и входят в эти формулы с отрицательным знаком.
Введем систему координат Oxy соответственно показанному на рисунке. Для проведения вычислений определим углы a0, b и g :
Sina0=0.5/1=0.5, то есть угол a0=p/6 (Cosa0=0.866 ).
Угол g=(p/2)-b, это означает, что Sing=Cosb=![]() =0.894,
Cosg=Sinb=
=0.894,
Cosg=Sinb=![]() =0.447
=0.447
Координаты центров масс частей фигуры в выбранной системе координат и их площади имеют значения:
x1=1 м, y1=1 м, S1=4 м2;
x2=2+(4/3p)R=2.42 м, y2=1 м, S2=pR2/2= 1.57 м2;
x3=0.5 м, y3=1.5 м, S3=pR2 =0.196 м2;
x4=2*(1/3)= 0.67м, y4=0.33 м, S4=(2*1)/2=1 м2;
x5=1+CD*Cosg=1+0.1699*0.447=1.076 м, y5=0.5+CD*Sing =0.5+0.1699*0.894=0.6519 м, S5=pR2/2=0.2512 м2;
x6=2+0.3+(1*Cosa0-0.3)/2 =2.583 м, y6=1 м, S6=0.566 м2;
x7=2+0.958=2.958 м, y7=1 м, S7=0.023 м2;
ПРИМЕЧАНИЯ: При вычислении положения центра масс полудиска [5] определяем его расстояние CD от центра полудиска по стандартной формуле. Размер и положение центра масс «вычитаемого» прямоугольника [6] определяем с помощью формул элементарной геометрии и данных для угла a0. Положение центра масс «вычитаемого» сегмента [7] с углом раствора 2a0 и радиусом R=1м определяем с помощью стандартной формулы, площадь сегмента определяем как разность площадей сектора с углом раствора p/3 и треугольника с основанием 1м и высотой 0.866 м.
Подставим полученные значения в формулы (1) и найдем координаты центра масс С фигуры:
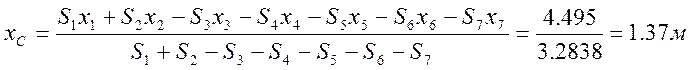 ;
;
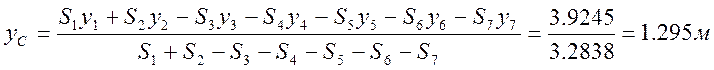 .
.
Решение задачи c)
Для определения положения центра масс объемной фигуры воспользуемся формулами :
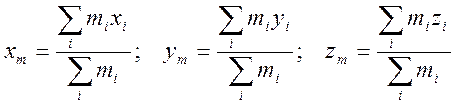 (1)
(1)
В качестве массы будем использовать пропорциональную ей величину – объем элементов.
Нашу фигуру можно представить в следующем виде:
Фигура = [1]Параллелипипед (20х30х15) + [2]Призма (20х30х15) –[3]цилиндр (h=15, d=10)
В формулах считаем, что «вычитаемые» части имеют отрицательную массу и входят в эти формулы с отрицательным знаком.
Введем систему координат Oxyz соответственно показанному на рисунке.
Координаты центров масс частей фигуры в выбранной системе координат и их объемы имеют значения:
x1=15 см, y1=10 см, z1=7.5 см, V1=9000 cм3;
x2=(30+1/3*30)=40 см, y2=10 см, z2=(1/3*15)=5 см, V2=4500 cм3;
x3=20 см, y3=10 см, z3=7.5 см, V3=p R2 h= 1177.5 cм3;
ПРИМЕЧАНИЕ: Призма 2 в сечении плоскостью, параллельной плоскости Oxz, представляет собой прямоугольный треугольник. Центр масс треугольника лежит на пересечении его медиан, то есть на расстоянии 1/3 от вершины треугольника с прямым углом по осям x и z соответственно.
Подставим полученные значения в формулы (1) и найдем координаты центра масс С фигуры:
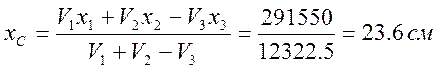
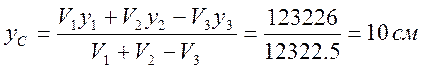
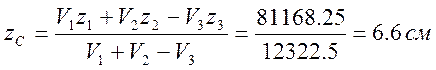
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.