Глава 17
Операционное исчисление
17.1. Нахождение изображений
17.1.1. Определение оригинала и изображения
Определение 1.
Функцией – оригиналом называется любая комплекснозначная функция ![]() действительного аргумента t, удовлетворяющая условиям: а)
действительного аргумента t, удовлетворяющая условиям: а) ![]() при
при ![]() , причем
принимается, что
, причем
принимается, что ![]() ; б) на любом конечном отрезке
; б) на любом конечном отрезке ![]() функция
функция ![]() может
иметь лишь конечное число точек разрыва первого рода; в)
может
иметь лишь конечное число точек разрыва первого рода; в) ![]() возрастает не быстрее показательной
функции: существуют такие постоянные M и
возрастает не быстрее показательной
функции: существуют такие постоянные M и ![]() , что
, что
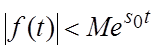 при
при ![]() ;
(1.1)
;
(1.1)
![]() называется показателем роста
функции
называется показателем роста
функции ![]() .
.
Простейшей функцией – оригиналом является единичная функция Хевисайда
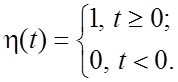 (1.2)
(1.2)
Для выполнения условия а) полагают
функцию ![]() равной
равной ![]() . Имея
в виду это замечание, множитель
. Имея
в виду это замечание, множитель ![]() обычно не пишут (если
не имеет место запаздывание аргумента – см. ниже, -где наличие множителя
обычно не пишут (если
не имеет место запаздывание аргумента – см. ниже, -где наличие множителя ![]() обязательно).
обязательно).
![]() Пример 1.
Показать, что функция
Пример 1.
Показать, что функция 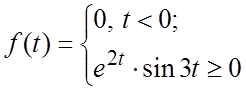 является оригиналом.
является оригиналом.
Решение. Условия а) и б),
очевидно выполнены. Условие в) выполнено в силу оценки 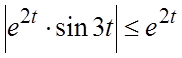 ,
так что в качестве M
в этом условии можно взять любое число, большее или равное единице;
,
так что в качестве M
в этом условии можно взять любое число, большее или равное единице; ![]() =2.
=2.
Определение 2.
Преобразованием Лапласа функции-оригинала ![]() называется
функция
называется
функция ![]() комплексной переменой
комплексной переменой ![]() , определяемая интегралом Лапласа
, определяемая интегралом Лапласа
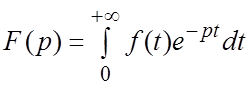 .
(1.3)
.
(1.3)
Теорема. Если ![]() - оригинал, то функция
- оригинал, то функция ![]() (интеграл (1.3) – преобразование Лапласа
функции
(интеграл (1.3) – преобразование Лапласа
функции![]() ) существует и аналитична в полуплоскости
) существует и аналитична в полуплоскости ![]() .
.
Определение 3. В
случае существования интеграл (1.3) называется изображением функции ![]() . Соответствие между оригиналом
. Соответствие между оригиналом ![]() и его изображением
и его изображением ![]() символически
записывается в виде
символически
записывается в виде ![]()
![]()
![]() .
.
Если ![]() -
изображение, то
-
изображение, то
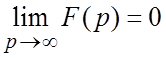 -
(1.4)
-
(1.4)
необходимое условие существования изображения.
Пример 2. Найти изображение функции Хевисайда (1.2).
Решение. Функция Хевисайда является оригиналом с
показателем роста ![]() . Имеем по формуле (1.3):
. Имеем по формуле (1.3):
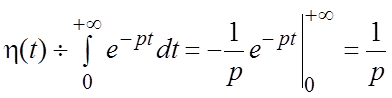 .
(1.2¢)
.
(1.2¢)
Пример 3. Могут ли функции а) ![]() , б) p, в)
, б) p, в) ![]() быть изображениями каких-либо
оригиналов?
быть изображениями каких-либо
оригиналов?
Решение. а) да, функция ![]() аналитична в полуплоскости
аналитична в полуплоскости ![]() ; необходимое условие для нее выполняется;
б) нет, не выполнено необходимое условие (1.4); в) нет: из аналитичности F(p) в полуплоскости
; необходимое условие для нее выполняется;
б) нет, не выполнено необходимое условие (1.4); в) нет: из аналитичности F(p) в полуплоскости ![]() следует,
что все особые точки функции F(p) должны лежать левее прямой
следует,
что все особые точки функции F(p) должны лежать левее прямой![]() или на самой прямой. По этой причине функция
или на самой прямой. По этой причине функция
![]() не является изображением: она имеет бесконечное
множество полюсов
не является изображением: она имеет бесконечное
множество полюсов 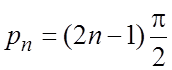
![]() ,
расположенных по всей оси Os.
,
расположенных по всей оси Os.
17.1.2. Свойства преобразования Лапласа. Таблица основных
изображений
Приведем свойства преобразования Лапласа и таблицу основных изображений, с помощью чего можно найти изображения большинства функций, встречающихся на практике.
А. Свойства преобразования
Лапласа. Отметим
симметричность свойств: каждому свойству оригиналов соответствует аналогичное
(“двойственное”) свойство изображений – см. свойства III и IV, V и VI, VII и VIII. Пусть ![]() ,
, ![]() .
.
I. Свойство линейности. Для любых комплексных постоянных ![]() и
и ![]()
![]() (1.5)
(1.5)
II. Теорема подобия. Для любого постоянного ![]()
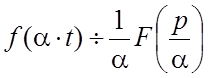 .
(1.6)
.
(1.6)
III. Дифференцирование оригинала. Если ![]() или
вообще
или
вообще ![]() является оригиналом, то
является оригиналом, то
![]() (1.7)
(1.7)
или
![]() . (1.7¢)
. (1.7¢)
IV. Дифференцирование изображения. Дифференцирование изображения сводится к умножению на –t оригинала
![]() ,
(1.8)
,
(1.8)
или вообще
![]() .
(1.8¢)
.
(1.8¢)
V. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на p:
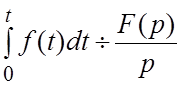 .
(1.9)
.
(1.9)
VI. Интегрирование изображения. Если интеграл 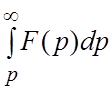 сходится, то он служит изображением
функции
сходится, то он служит изображением
функции 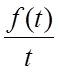 :
:
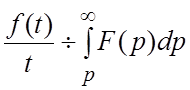 (1.10)
(1.10)
- интегрирование изображения равносильно делению на tоригинала.
VII. Теорема запаздывания. Включение оригинала с запаздыванием на
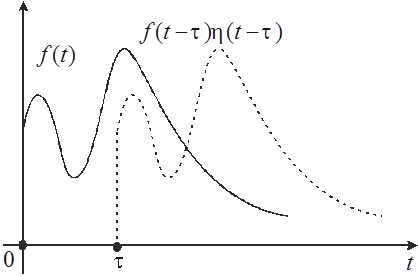 Рис.1.
Рис.1.
![]() (рис. 1) равносильно умножению
изображения на
(рис. 1) равносильно умножению
изображения на ![]() ; то есть
; то есть ![]()
![]() .
(1.11)
.
(1.11)
VIII. Теорема смещения. “Смещение” изображения на ![]() равносильно умножению оригинала на
равносильно умножению оригинала на ![]() ; то есть
; то есть ![]() (комплексного)
(комплексного)
![]() .
(1.12)
.
(1.12)
Определение. Сверткой функций-оригиналов ![]() и
и ![]() (обозначается
(обозначается
![]() ) называется интеграл
) называется интеграл
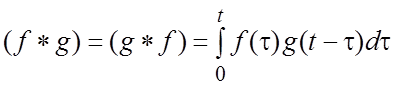 (1.13)
(1.13)
IX. Теорема умножения. Произведение двух изображений ![]() и
и ![]() также
является изображением, причем
также
является изображением, причем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.