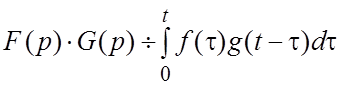Операционное исчисление. Нахождение изображений. Восстановление оригинала по изображению, страница 2

                                                                               (1.14)

-умножение изображений равносильно свертыванию оригиналов.

X. Интеграл Дюамеля. Интегралом Дюамеля называется каждая из равносильных четырех формул:

              

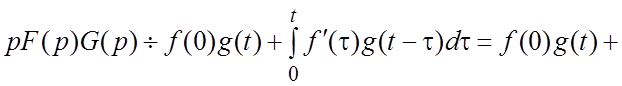
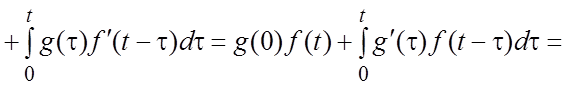                                             (1.15)

                               .

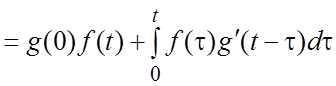Б. Приведем таблицу изображений “основных” функций:

                                                                                                               Таблица

№				№
1				6
2				7
3				8
4				9
5				10

17.1.3. Примеры вычислений изображений

          Пример 1. По определению (1.3) 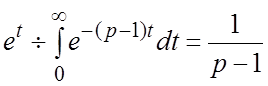 (2). Заметим, что из соответствия (1.2¢) и свойства (1.12) следует, что 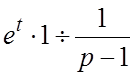. По свойству (1.6) из (2) получим  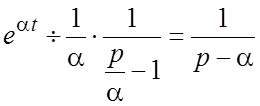   (3). Можно доказать, что это соответствие выполняется  комплексного (правее прямой ). Так как , то по свойству (1.5) получим:

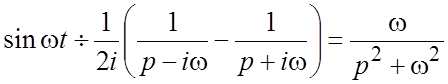                             .                                        (4)

          Пример 2. Полагая в формуле (1.8¢) , получим изображение натуральной степени t: 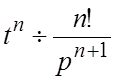 (5). Приняв , получим в силу (3)

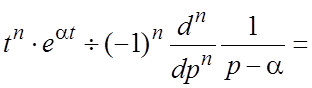
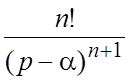 . (6)

          Пример 3. Найти изображение оригинала .

          Решение. Применяя (6), (5), (1.2¢) и свойство линейности (1.5), получим

                        .

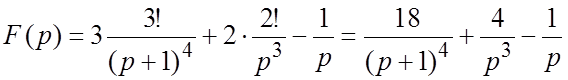          Пример 4. Найти изображение .

          Решение. Проверка показывает, что функция 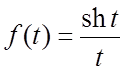 является оригиналом (удовлетворяет трем условиям а) - в); следует учесть, что 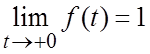). Для оригинала  имеем: 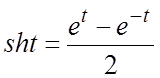 и по свойству (1.5) получим соответствие (найдем его изображение): 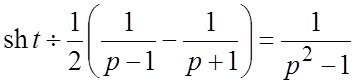. Применяя свойство (1.10), получим .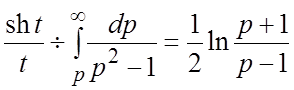

          Пример 5. Найти изображение дифференциального выражения , если , , ; .

          Решение. По свойству (1.7) и (1.7¢) получим: ; ;   и 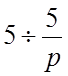. По свойству (1.5)  .

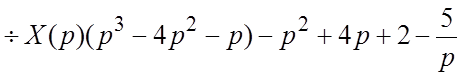          Пример 6. Построить график функции  и найти его изображение.

Рис.2.

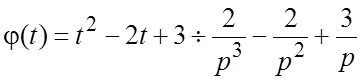          Решение. Функция  описывает некоторый процесс, “включаемый” с запаздыванием . Для того, чтобы решить, какой это процесс, нужно заданную функцию представить в форме ; иначе, следует представить функцию  по формуле Тейлора по степеням разности . Имеем: ;  ;   и  ; то есть  есть процесс , “включаемый” с запаздыванием . На рис. 2 представлены графики функций  и . Так как , то по свойству (1.11) находим:

.

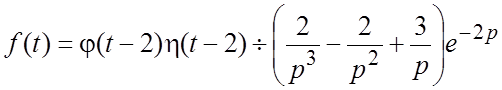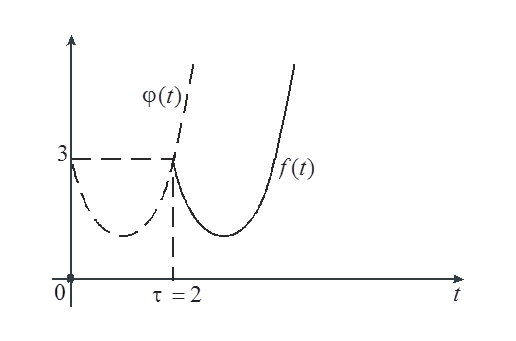
          Пример 7. На рис. 3 представлен график функции :

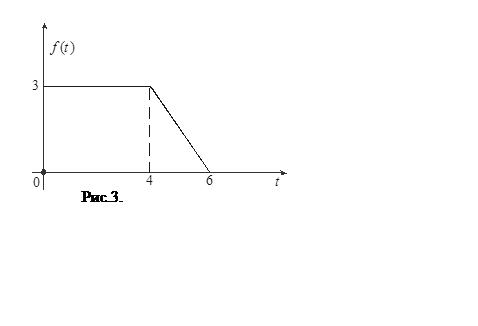
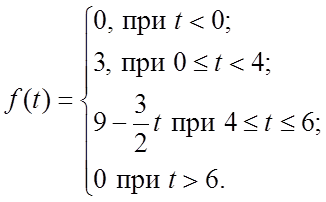
С помощью единичной функции Хевисайда записать одним аналитическим выражением и найти изображение этой функции.

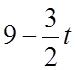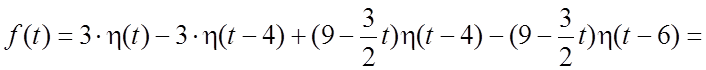
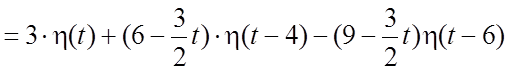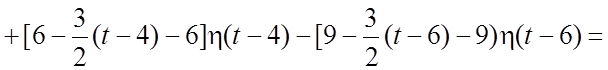
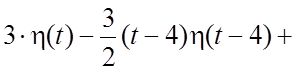
          Решение.  при ; в момент  “включается” функция, равная 3, в момент  она “гасится” и “включается’ функция ; в момент  “гасится” и эта функция. Всю эту последовательность действий можно записать следующим образом:  . Для того, чтобы найти изображение этой функции, нужно. рассуждая как и в примере 6, представить ее в форме: . Имеем   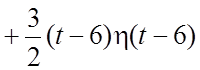. Так как , , 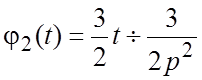то по свойству (1.11) находим: .

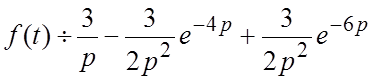17.2.    Восстановление оригинала по изображению

1. Элементарный метод. В некоторых случаях заданное изображение  может быть преобразовано к такому виду, когда оригинал легко восстанавливается непосредственно с помощью свойств преобразования Лапласа и таблицы изображений “основных” функций. Для преобразования изображения , являющегося правильной рациональной дробью, в этом случае используется метод разложения ее в сумму простейших дробей; далее находят оригинал для каждой  простейшей дроби, используя свойства I – IX преобразования Лапласа.

          Пример 1. Найти оригинал по изображению .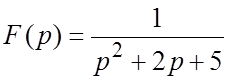

          Решение. Первый способ. Выделяя полный квадрат в знаменателе и далее, используя табличное изображение для  и теорему смещения, получим: 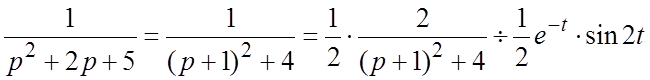. Второй способ. Раскладывая дробь в сумму простейших и используя изображение для , найдем:  .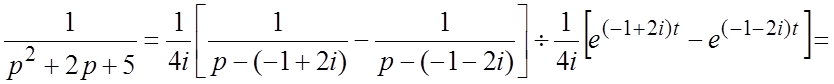

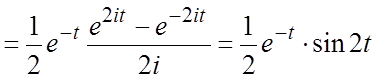          Пример 2. Найти оригинал, если .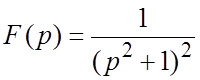

          Решение. Первый способ. Раскладываем дробь в сумму простейших: 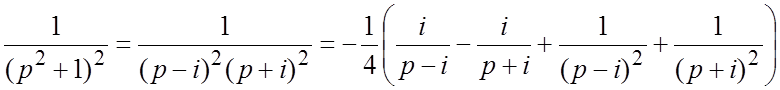 и следовательно, 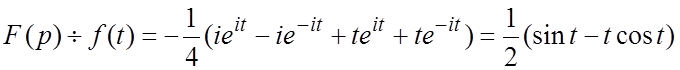. Второй способ. Заметим, что 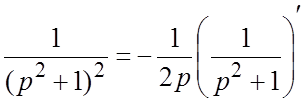. По теореме о дифференцировании изображения 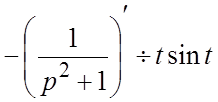. Применяя теперь теорему об интегрировании оригинала, находим: 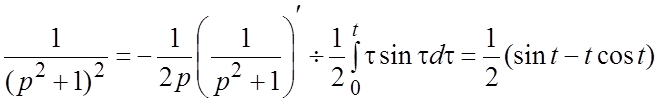.Третий способ. Используя свойство IX- теорему умножения, получим:

    .

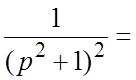
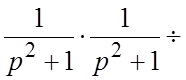
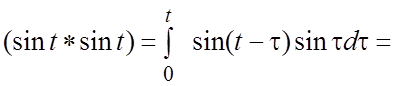
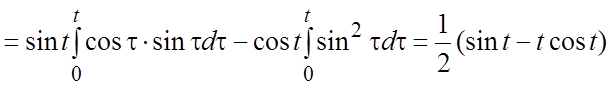          Пример 3. Найти оригинал по изображению .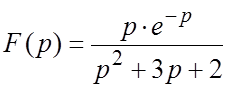

          Решение. Сначала разложим дробь 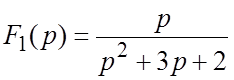 на элементарные: 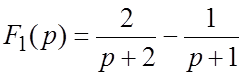. Найдем оригинал: . На основание теоремы запаздывания  имеем .

2. Теоремы   разложения. Отыскать оригинал по его изображению в некоторых случаях удается с помощью так называемых теорем разложения.

          Первая теорема разложения. Если функция  аналитична в бесконечно удаленной точке , то есть разложение этой функции в ряд Лорана в окрестности этой точки имеет вид

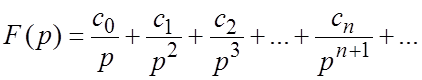                                     ,                                (2.1)  

то  является изображением оригинала , определяемого степенным рядом

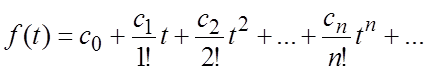                                                                     (2.2)

Пример 1. Найти оригинал по изображению .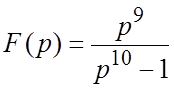

Решение. Разложим данную дробь по отрицательным степеням p:   

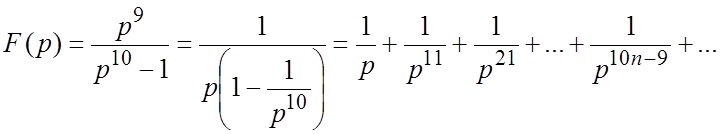   (при ).

Пользуясь первой теоремой разложения отсюда получим