Нелинейные системы автоматического регулирования. Типы особых точек и фазовые портреты линейных систем

Нелинейные системы автоматического регулирования [5].

Статическая нелинейность – это нелинейность статической характеристики звена. Эти характеристики могут быть непрерывными или релейными, однозначными или с гистерезисом.

Если динамика звена системы описывается нелинейным дифференциальным уравнением, то это – динамическая нелинейность. Нелинейным является, например, уравнение движения системы при наличии вязкого или сухого трения, или уравнение, параметры которого зависят от значений переменных. Заметим, в линейных системах с переменными параметрами последние зависят от времени, в нелинейных – от координат.

Нелинейности в системах регулирования могут быть естественными и специально вводимыми для придания системе желаемых свойств.

Фазовая плоскость.

При составлении уравнений динамики системы все звенья, поддающиеся линеаризации, описываются линейными уравнениями. И только для одного-двух существенно нелинейных звеньев составляются нелинейные уравнения, или используются нелинейные характеристики. Общий вид нелинейного дифференциального уравнения:

, .

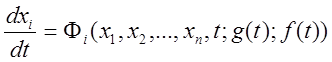Пространство координат состояния системы () называется фазовым пространством, в котором решение уравнения движения изображается в виде фазовой траектории системы. Заметим, что  – проекции скорости изображающей точки – текущей точки фазовой траектории.

Ниже будут рассматриваться только системы второго порядка, которым соответствуют двухмерные пространства состояний – фазовые плоскости.

Уравнения движения стационарной системы в отсутствие внешних воздействий:

, .

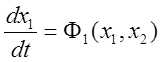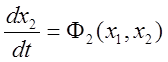Дифференциальное уравнение фазовой траектории получается путём исключения времени из этой системы уравнений:

.

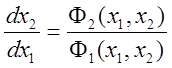Точки равновесного состояния определяются нулевыми значениями скоростей , . Следовательно

, ,

что создаёт неопределённость правой части уравнения фазовой траектории. Поэтому точки равновесного состояния являются особыми точками на фазовой плоскости.

Пусть уравнения движения системы имеют вид:

, .

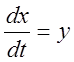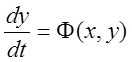Т.е. координата y, откладываемая по оси ординат, представляет собой скорость изменения координаты x, откладываемой по оси абсцисс.

Сопоставим изображение в виде фазовых траекторий на плоскости  с обычным его представлением в виде кривой . В этом случае для изображающей точки справедливо следующее: изображающая точка движется в верхней полуплоскости слева направо, так как там , а в нижней – справа налево, так как там ; ось x пересекается фазовыми траекториями под прямым углом, так как там скорость , т.е. имеет место максимум или минимум величины x.

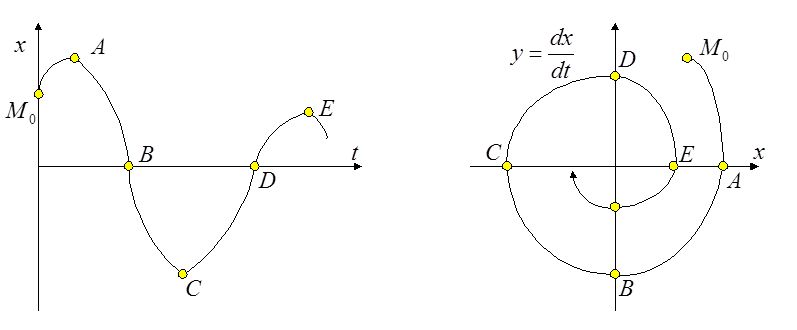
В общем случае это правило недействительно.

Видно, что затухающий (нарастающий) колебательный процесс соответствует на фазовой плоскости сходящейся (расходящейся) спирали. Периодический процесс изобразится в виде замкнутой кривой. Монотонно затухающий (нарастающий) процесс изобразится на фазовой плоскости в виде кривой, монотонно приближающейся (удаляющейся) к положению равновесия.

Типы особых точек и фазовые портреты линейных систем.

Уравнения линейной системы второго порядка имеют вид:

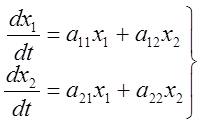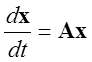, или , где 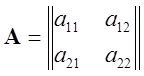, при условии .

Дифференциальное уравнение фазовых траекторий:

.

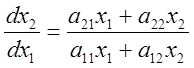Единственная особая точка , . Характеристическое уравнение:

.

Пусть его корни  различны. Путём подстановки  исходная матрица приводится к диагональному виду. Уравнения движения примут вид:

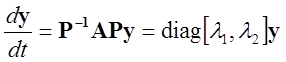, или , .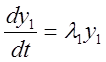

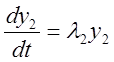Решения:

, .

Случай вещественных корней.

Пусть . Исключая время, получим уравнение фазовой траектории:

.

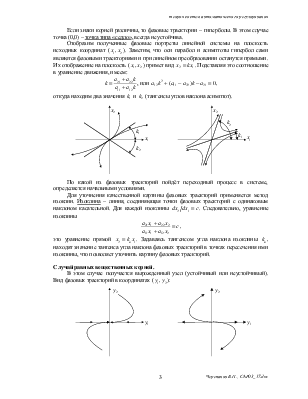
Если знаки корней одинаковы, то фазовые траектории – параболы. Направление движения изображающей точки определяется знаками корней. Если корни отрицательны (положительны), то точка (0,0) называется точкой типа «устойчивый (неустойчивый) узел».

Если знаки корней различны, то фазовые траектории – гиперболы. В этом случае точка (0,0) – точка типа «седло», всегда неустойчива.

Отобразим полученные фазовые портреты линейной системы на плоскость исходных координат (). Заметим, что оси парабол и асимптоты гипербол сами являются фазовыми траекториями и при линейном преобразовании останутся прямыми. Их отображение на плоскость () примет вид . Подставляя это соотношение в уравнение движения, имеем:

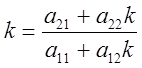, или ,

откуда находим два значения  и  (тангенсы углов наклона асимптот).

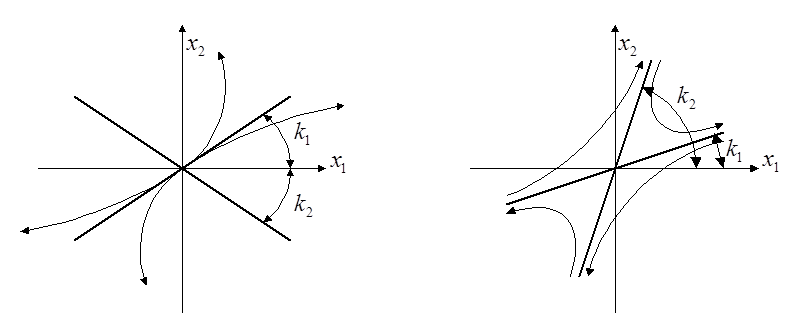
По какой из фазовых траекторий пойдёт переходный процесс в системе, определяется начальными условиями.

Для уточнения качественной картины фазовых траекторий применяется метод изоклин. Изоклина – линия, соединяющая точки фазовых траекторий с одинаковым наклоном касательной. Для каждой изоклины . Следовательно, уравнение изоклины

,

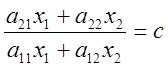это уравнение прямой . Задаваясь тангенсом угла наклона изоклины , находят значение тангенса угла наклона фазовых траекторий в точках пересечения ими изоклины, что позволяет уточнить картину фазовых траекторий.

Случай равных вещественных корней.

          В этом случае получается вырожденный узел (устойчивый или неустойчивый). Вид фазовых траекторий в координатах ():

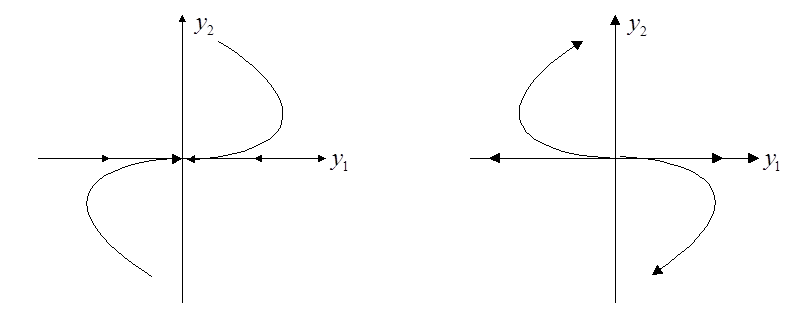
Случай комплексных корней.

Переходной процесс – колебательный. Пусть . Решения:

, .

Введя новые переменные , , преобразуем решения к вещественной форме:

, .

В полярных координатах ():

, , .

Эти выражения описывают логарифмическую спираль. При отрицательной (положительной) вещественной части корней точка (0,0) называется «точкой типа устойчивый (неустойчивый) фокус».

Необходимо, однако, преобразовать полученные фазовые портреты в исходную систему координат. Для этого воспользуемся методом изоклин.

Пусть, например, задана система

.

Корни характеристического уравнения . Обозначив , , приведём систему к виду

, .

Дифференциальное уравнение фазовых траекторий:

.

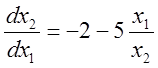Для изоклины  находим . Возьмём изоклины с . Тогда . Соответствующие направления касательных к фазовым траекториям показаны стрелками на рисунке:

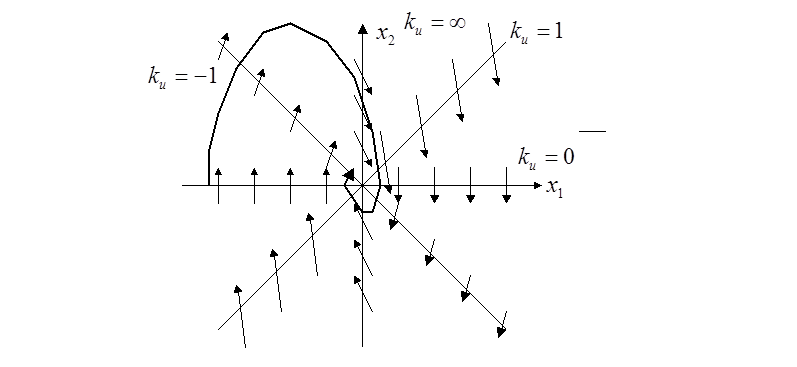
При чисто мнимых корнях здесь получатся эллипсы. Особая точка (0,0) в этом случае называется «точкой типа центр».