Момент силы относительно точки и оси, пара сил

§ 1.4. Момент силы относительно точки и оси, пара сил

1. Алгебраический момент силы относительно точки. Используется при рассмотрении плоской системы сил. Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус. Плечом hсилы F называют кратчайшее расстояние между этой точкой и линией действия силы. Знак зависит от направления "вращения" тела относительно точки: Q - (+), P - (-).

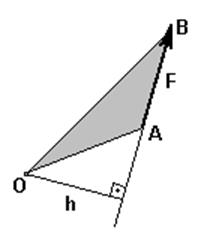
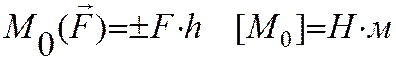
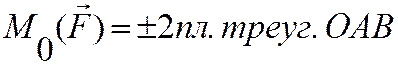
2. Векторный момент силы относительно точки. Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть "стремление" силы вращать тело против движения часовой стрелки.

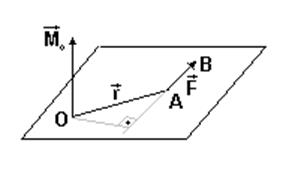
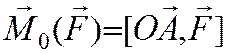
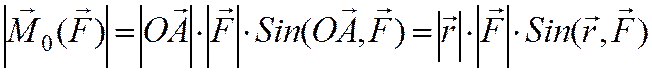
            Векторный момент силы относительно точки не меняется при скольжении силы  по линии действия и равен нулю, если линия проходит через точку О.

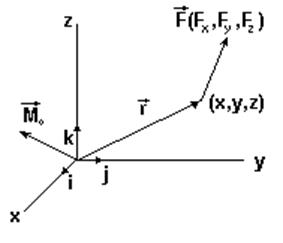
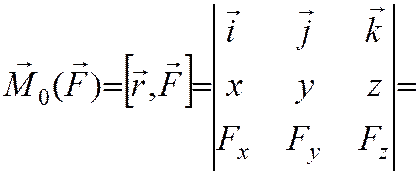
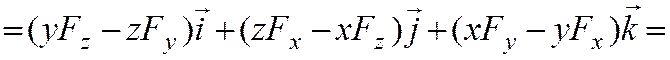
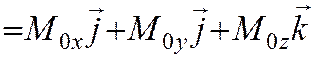
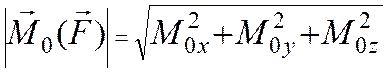
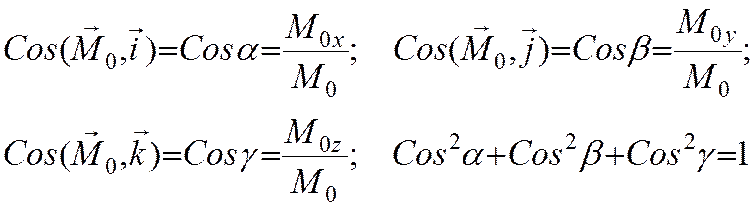
            Косинусы углов a,b,g суть проекции на оси координат единичного вектора, направленного по вектору момента M₀.

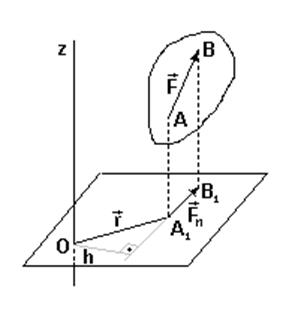3. Момент силы относительно оси. Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью. Знак определяется направлением вращения (Q - (+), P - (-)).

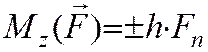
Свойства:       а) M_z=0, если сила параллельна ост Oz

                        б) M_z=0, если линия действия пересекает ось Oz

Короче говоря, момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

4. Связь момента силы относительно оси с векторным моментом силы относительно точки на оси.

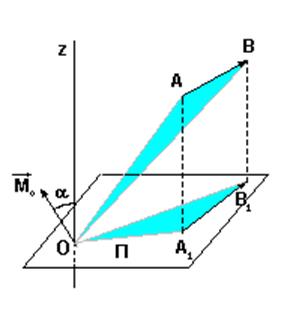
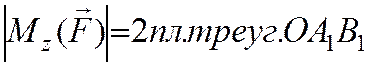
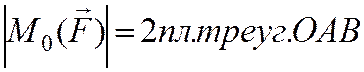
            Треугольник OA₁B₁ является проекцией треугольника OAB на плоскость П. Из стереометрии известно, что площадь проекции плоской фигуры равна площади проецируемой фигуры, умноженной на косинус угла между плоскостями, в которых расположены эти фигуры (или косинус угла между нормалями к плоскостям этих фигур, т.е.  и ).

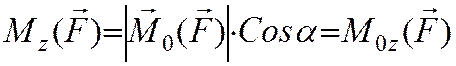
            Окончательно: момент силы относительно оси равен проекции на эту ось векторного момента силы относительно любой точки на оси.

Тогда имеем:

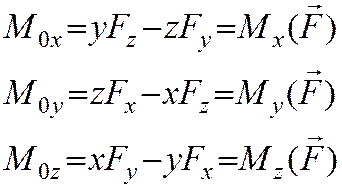
5. Пара сил и алгебраический момент пары сил.

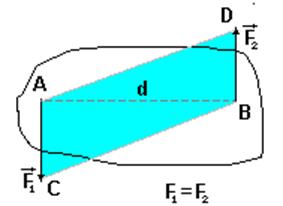
            Парой сил называют систему двух равных по модулю параллельных сил (не лежащих на одной прямой), направленных в противоположные стороны.

            Обычно пару сил прилагают к телу, которое должно вращаться.

            Пару сил нельзя заменить одной силой, т.е. она не имеет равнодействующей и является такой системой сил, которую упростить нельзя.

            Пара сил, действующая на твердое тело, характеризуется плоскостью действия (сила – линией действия)

Определение Алгебраическим моментом пары сил называют взятое со знаком (+) или (-) произведение модуля одной из сил пары на плечо пары сил (расстояние между линиями действия сил пары).

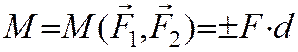
            Знак (+), как обычно, мы приписываем моменту, если пара "стремится" вращать тело против часовой стрелки, (-) – для вращения по часовой стрелке.

Алгебраический момент пары сил не зависит от переноса сил пары вдоль своих линий действия. Алгебраический момент пары сил численно равен (со знаком (+) или (-)) площади параллелограмма ACDB или удвоенной площади треугольников ABC или ABD.

Две пары сил называют эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема.

Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой сил алгебраический момент (Две пары сил, расположенные в одной плоскости, эквивалентны, если они имеют одинаковые алгебраические моменты)

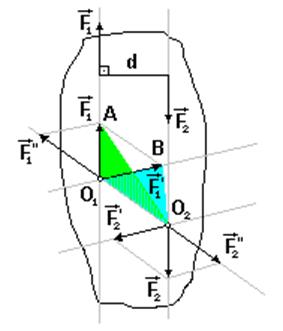
            Доказательство: Перенесем силы F₁, F₂ исходной пары вдоль их линий действия в новые произвольные точки О₁, O₂. Проведем через эти точки прямую О₁О₂ и две произвольные параллельные прямые. Разложим вектора F₁ и F₂ в точках О₁ и О₂ на F₁',F₁" и F₂',F₂" в направлении на эти прямые. Силы F₁", F₂" образуют "нулевую" систему сил, которую можно отбросить. У нас остается пара сил F₁',F₂' с новым плечом и новыми модулями сил. Эта пара сил  эквивалентна исходной, т.к. при всех преобразованиях мы не нарушали условие эквивалентности систем сил:

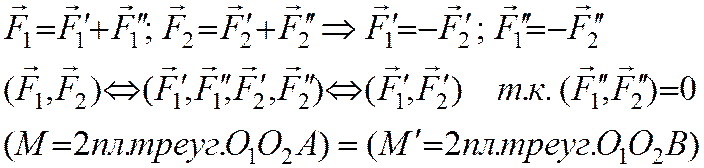
            Момент новой пары сил равен моменту исходной пары сил.

Выводы:

а) пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия,

б) у пары сил можно изменять плечо и модули сил, сохраняя при этом алгебраический момент пары и плоскость действия.

Эти манипуляции над парами сил не изменяют их действия на твердое тело.

Теорема.  Действие пары сил на твердое тело не изменяется от переноса этой пары сил в параллельную плоскость (без доказательства, доказательство может быть проведено методами, аналогичными методам из предыдущей теоремы).

            Плоскость действия, момент и направление вращения пары можно определить через векторное произведение.

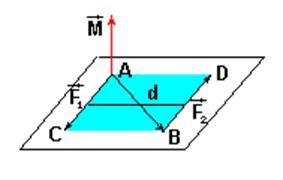
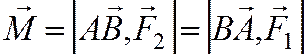
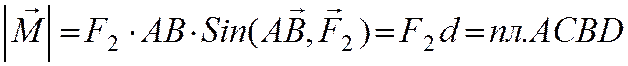
Векторный момент пары сил, действующей на твердое тело есть свободный вектор (точкой приложения может быть любая точка тела).

Теорема. Сумма векторных моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора точки и равна векторному моменту этой пары сил.

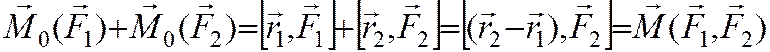
            Для сложения двух пар сил, лежащих в пересекающихся плоскостях, надо сложить их векторные моменты в любой точке по правилу параллелограмма (так как вектора моментов – вектора свободные).

            Таким образом, 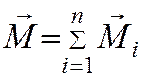 для n произвольно расположенных пар.

            Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций векторных моментов пар сил на каждую из трех координатных осей была равна нулю.