Определение количества молекулярных термов. Определение распределения спиновой плотности в радикале

Задачи для контрольной по “Строению вещества” 30 декабря 1995 г.

1. (200) Определить количество молекулярных термов, которые могут возникнуть при сближении двух ионов Fe²⁺ (3d⁶ конфигурация) в основных состояниях и при образовании молекулярного иона Fe²⁺-Fe²⁺.

2. (300) Определить на какие неприводимые представления распадется Т₂ представление группы Т_d при понижении симметрии от Т_d до C_3v.

3. (400) Определить термы (тип и количество) основной электронной конфигурации для плоской p-системы, показанной на рисунке.

4. (300) Определить распределение p-заряда в p-системе молекулы H₂C-O-CH₂, образованной атомами C, O и С (a_o = a_c + 2b). Учесть, что p-орбиталь кислорода поставляет два электрона.

5. (800) В циклическом p-радикале, состоящем из N центров, к одному из центров (обозначим его за номер 1) вводится индуктивный заместитель (CH₃-группа, x=-0.1). Определить (количественно), как изменится спиновая плотность на этом центре при присоединении заместителя. Привести ответ для N = 99 и N =101.

Задачи для контрольной 30 декабря 1996 года

1. (300) Для циклической p-молекулы, состоящей из N p-центров с одним CH₃ заместителем определить направление преимущественного электрофильного замещения (выбор между центрами 2 и 3?). Что будет, если в этой молекуле два CH₃ заместителя, присоединеных к соседним центрам (см. рисунки).

2. (200) Определить распределение спиновой плотности в радикале H₁₅, строение которого представлено на рисунке.

3. (600) Определить термы, между которыми происходит самый длинноволновый переход, его энергию (выразить через резонансные интегралы) и поляризацию для радикала H₈, строение которого показано на рисунке.

4. (400) Определить основной терм линейного кластера, состоящего из четного числа (N) ионов Fe³⁺ (электронная конфигурация 3d⁵), содержащего еще один дополнительный электрон.

5. (500) С помощью теории возмущений определить вид и энергию нижней орбитали p-системы молекулы нафталина.

Задачи на контрольную 29 декабря 1997 года, группы 541-542-446.

1. (400) Определить распределение спиновой плотности для бензильного радикала по теории возмущений, считая, что к p-системе бензола присоединяется CH₂-группа. Сравнить с точным решением.

2. (600) Определить вид, симметрию и энергию молекулярных орбиталей для молекулы H₆, имеющей строение правильного октаэдра (см. рисунок). Показать разрешенные переходы. Между атомами, находящимися на одной оси, связи нет.

3. (500) Определить распределение спиновой плотности для анион-радикала H₈^-, строение которого представлено на рисунке. Резонансные интегралы между всеми связанными центрами считать одинаковыми.

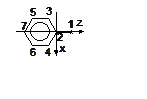
4. (300) Определить направление преимущественного электрофильного замещения в молекуле замещенного циклобутадиена (СН₃С₄Н₃).

5. (200) Рассчитать величины p_rs для этилена и определить распределение заряда в замещенном этилене (см. рисунок).

Задачи на контрольную 27 декабря 1998 г., группы 641, 642, 546.

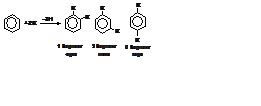1. (500) Определить энергию, вид и симметрию самой нижней молекулярной орбитали p-системы бензильного радикала.

2. (400) Определить предпочтительное направление одновременного радикального замещения в молекуле бензола двух атомов водорода.

3. (200) Определить возможные термы, возникающие при сближении атома Н и иона ОН⁺ с образованием линейного иона НОН⁺. Будет ли среди найденных термов основной терм этого иона?

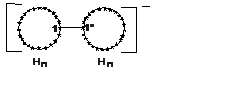
4. (700) По теории возмущений определить спиновую плотность на эквивалентных центрах 1 и 1’ (см. рисунок) для иона Н_2n^-, где n = 4k+2 (k – целое число). Чему будет равна спиновая плотность на этих центрах при n>>1.

5. (200) Определить электронную конфигурацию и основной терм линейной молекулы Li-C-Li.

Задачи на контрольную 30 декабря 1999, группы 741, 742, 646

1. (500) В группе есть 2 одномерных и 2 двухмерных неприводимых представления. Определить распределение операций симметрии по классам и построить таблицу характеров для данной группы.

2. (300) Определить относительную устойчивость p-систем изомеров 1, 2 и 3 (рисунок).

3. (600) Определить распределение спиновой плотности в анион-радикале C₈H₈^- (рисунок). Найти точное решение и по теории возмущений.

4. (300) Определить преимущественное направление радикального замещения по центрам 3 и 5 для молекулы C₆H₆ (рисунок). Отметим, что в этой молекуле 1 не заместитель, а группа CH₂ с p-центром. Неэквивалентность центров 3 и 5 создается геометрией молекулы.