Определение количества молекулярных термов. Определение распределения спиновой плотности в радикале, страница 4

Решение: Разрежем тетрацен на три четных p-системы, каждая из которых содержит по 6 центров (бензол + 6 + бензол), как показано на рисунке. Орбитали бензола представлены в методичке. Найдем для центральной p-системы нижнию по энергии орбиталь. Для этой ситемы по одному представлению (группы D_2h) будут преобразовываться комбинации

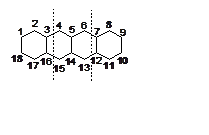
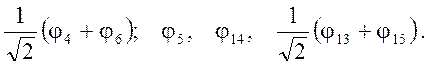
Для них детерминант имеет вид 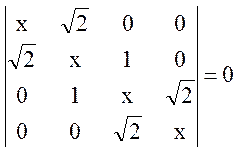, корни которого Нижняя по энергии орбиталь имеет корень  (энергия E = a +2b). Подставляя это значение в детерминант, получим коэффициенты в линейной комбинации, определяющей вид нижней орбитали радикала

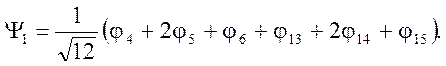
Таким образом все три части имеют нижние орбитали с одинаковой энергией, то есть эти орбитали вырождены. Вводим возмущение в виде связывания центров 3-4, 6-7, 12-13, 15-16 (напрмер, <j₃|V|j₃> = b), и решаем задачу теории возмущений для вырожденного случая с детерминантом 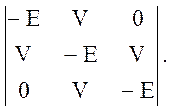 Этот детерминант имеет корни E = 0, ±Ö2 V, где 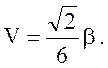Нижний корень E = Ö2 V (V – отрицателен, как и b). Подставляя этот корень в детерминант, получим соответствующую общую молекулярную орбиталь 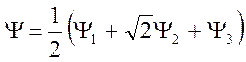, где первая и третья орбитали молекул бензола, а вторая – орбиталь центральной системы (найдена выше). Подставляя все эти орбитали в общее выражение, получим

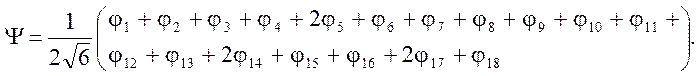
Энергия нижней орбитали будет равна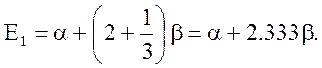

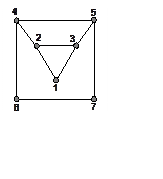4. (400) Близится новый год – год обезьяны. Определите распределение спиновой плотности в p-системе из 7 p-центров, которая чем-то похожа на голову обезьяны (см. рисунок). Все резонансные интегралы считать одинаковыми.

Решение: Для определения МО используем симметрию. По одному представлению будут преобразовываться комбинации

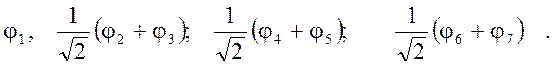
По другому представлению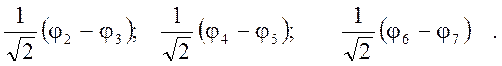

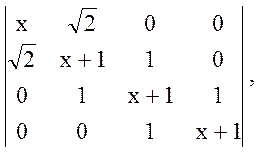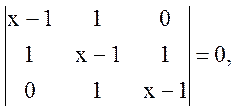Для первого набора функций детерминант имеет вид  для второго . Для первого детерминанта корни  для второго –  Анализ показывает, что неспаренный электрон находится на вырожденных орбиталях x = 1 (E = α - b). Подставляя это значение в первый детерминант, находим коэффициенты и вид первой орбитали неспаренного электрона

 

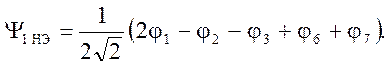
Подставляя x = 1 во второй детерминант, получим

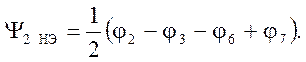
Считая заселенности этих орбиталей по ½, получим распределение спиновой плотности, которое имеет вид r₁ = ¼,  r₂ = r₃ =r₆ = r₇  = 3/16.

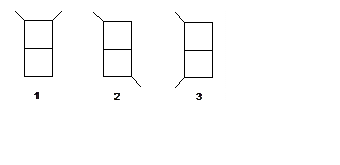5. (300) Определить относительную стабильность p-систем изомеров, которые представлены на рисунке.

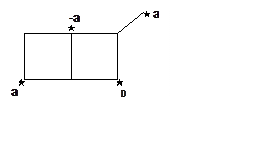Решение. Режем эти 8 центровые p-системы на два альтернантных радикала, а затем склеиваем их в исходные молекулы. Сперва режем на радикалы 1 + 7 (отрезаем один из “хвостиков”). Выигрыш в энергии при объединении p-систем радикалов в молекулы по теории возмущений равен DE = 2Sabb, где сумма по всем объединяющимся центрам, а a и b – коэффициенты при соответствующих центрах в орбитали неспаренного электрона. Простой расчет вида орбиталей неспаренного электрона для 7-центрового радикала (звездочками отмечены центры, на которых есть неспаренная плотность) показывает, что при таком разрезании DE₁ = DE₃ = 0, DE₂ = (2/Ö3)b и 2-ой изомер более стабилен.

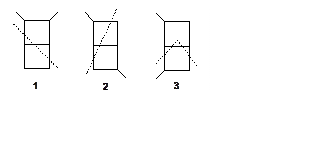Разрезание на радикалы 5 + 3, как показано на следующем рисунке, приводит к величинам DE₁ = DE₃ = 0, DE₂ = b. Таким образом, при этом разрезании вторая p-система также более устойчива.

Решение задач контрольной 28 декабря 2004 года. Группы 241-243

1. (400) Построить таблицу характеров для абелевой группы, в которой имеется три операции симметрии.

Решение: В группе три операции, три класса и три одномерных представления, одно из которых является полносимметричным (все характеры единицы). Таблица характеров будет иметь вид

	E	R1	R2
A1	1	1	1
Г1	1	X1	X2
Г2	1	X3	X4