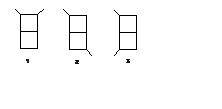
 4. (400) Близится новый год – год обезьяны.
Определите распределение спиновой плотности в p-системе из
7 p-центров, которая чем-то похожа на голову обезьяны
(см. рисунок). Все резонансные интегралы считать одинаковыми.
4. (400) Близится новый год – год обезьяны.
Определите распределение спиновой плотности в p-системе из
7 p-центров, которая чем-то похожа на голову обезьяны
(см. рисунок). Все резонансные интегралы считать одинаковыми.
5. (300) Определить относительную стабильность p-систем изомеров, которые представлены на рисунке.
Задачи на контрольной 28 декабря 2004 года. Группы 241-243
1. (400) Построить таблицу характеров для абелевой группы, в которой имеется три операции симметрии.
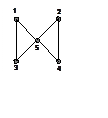
 2. (400) Для радикала H5,
строение которого показано на рисунке (плоская частица), определить число линий
поглощения, соответствующих разрешенным переходам, поляризацию и энергию этих
линий. Все резонансные интегралы считать одинаковыми.
2. (400) Для радикала H5,
строение которого показано на рисунке (плоская частица), определить число линий
поглощения, соответствующих разрешенным переходам, поляризацию и энергию этих
линий. Все резонансные интегралы считать одинаковыми.
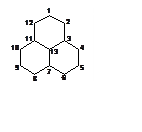
 3. (400) По теории возмущений определить энергию и вид
молекулярной орбитали неспаренного электрона -радикала,
показанного на рисунке (разрезать на циклическую систему и изолированный 13
центр). Сравнить с точным решением.
3. (400) По теории возмущений определить энергию и вид
молекулярной орбитали неспаренного электрона -радикала,
показанного на рисунке (разрезать на циклическую систему и изолированный 13
центр). Сравнить с точным решением.
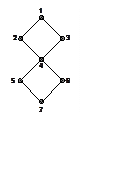
 4. (500)
Определите распределение спиновой плотности в радикале H7, строение которого показано на рисунке. Все
резонансные интегралы считать одинаковыми. Как изменится распределение спиновой
плотности, если первый атом водорода заменить на атом дейтерия?
4. (500)
Определите распределение спиновой плотности в радикале H7, строение которого показано на рисунке. Все
резонансные интегралы считать одинаковыми. Как изменится распределение спиновой
плотности, если первый атом водорода заменить на атом дейтерия?
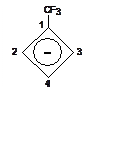
5. (300) Определить изменение спиновой плотности на 2-м центре циклобутадиенового анион-радикала при введении CF3 заместителя в первое положение (см. рисунок).
 Решение задач контрольной 29
декабря 2003 года. Группы 141-143
Решение задач контрольной 29
декабря 2003 года. Группы 141-143
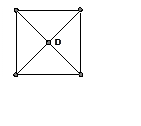
1. (500) Для радикала DH4, строение которого показано на рисунке (плоская симметричная частица), определить число линий поглощения, соответствующих разрешенным переходам, поляризацию и энергию этих линий, а также распределение спиновой плотности. Резонансные интегралы βHH и βHD считать одинаковыми.

Решение: Будем считать, что вместо атома дейтерия находится атом водорода, т.е.
рассмотрим радикал H5. Для этого радикала и данной группы симметрии
по A1g преобразуются комбинации
 По B1g
По B1g
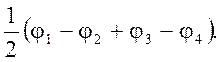 По Eu
По Eu 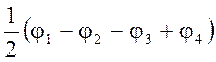 и
и 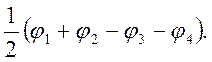 Для A1g
детерминант имеет вид
Для A1g
детерминант имеет вид 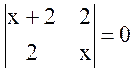 ,
который дает корни
,
который дает корни ![]() Подставляя эти корни в
детерминант, находим молекулярные орбитали, относящиеся к этому неприводимому
представлению (
Подставляя эти корни в
детерминант, находим молекулярные орбитали, относящиеся к этому неприводимому
представлению (![]()
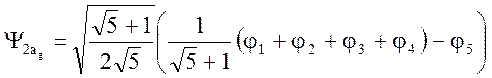 и
и ![]() ,
, 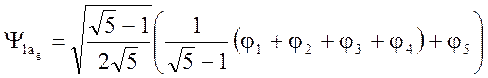 .
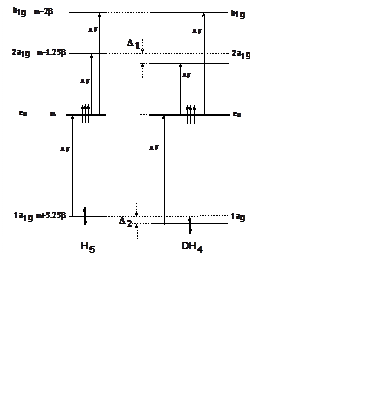
Энергии орбиталей Eu E = α (x = 0) и B1g E = α - 2b (x = 2). Окончательный вид и симметрия МО для радикала H5
показана на диаграмме уровней. Там же указаны разрешенные переходы и
поляризация. Появление в пятом положении атома дейтерия можно учесть по теории
возмущений, используя матричный элемент <φ5½V½φ5> = Da » a´(m/2M). Справа на диаграмме показано положение уровней для
DH4 радикала и разрешенные переходы с поляризацией. Для H5
радикала будет 3 линии с энергиями 1.23b (xy), 2b (xy) и 3.23b (xy). В скобках указана поляризация. Для DH4
радикала останется также 3 линии с энергиями 2b (xy), (1.23b - D1)
(xy), (3.23b + D2) (xy). где параметры D1 = 0.276Da и D2 = 0.72Da, Так как для DH4 радикала неспаренный
электрон находится на eu орбиталях, содержащих только 1-4 центры, спиновая
плотность будет только на этих центрах по r = ¼.
.
Энергии орбиталей Eu E = α (x = 0) и B1g E = α - 2b (x = 2). Окончательный вид и симметрия МО для радикала H5
показана на диаграмме уровней. Там же указаны разрешенные переходы и
поляризация. Появление в пятом положении атома дейтерия можно учесть по теории
возмущений, используя матричный элемент <φ5½V½φ5> = Da » a´(m/2M). Справа на диаграмме показано положение уровней для
DH4 радикала и разрешенные переходы с поляризацией. Для H5
радикала будет 3 линии с энергиями 1.23b (xy), 2b (xy) и 3.23b (xy). В скобках указана поляризация. Для DH4
радикала останется также 3 линии с энергиями 2b (xy), (1.23b - D1)
(xy), (3.23b + D2) (xy). где параметры D1 = 0.276Da и D2 = 0.72Da, Так как для DH4 радикала неспаренный
электрон находится на eu орбиталях, содержащих только 1-4 центры, спиновая
плотность будет только на этих центрах по r = ¼.
2. (300) Определить табличные значения поляризуемости p11 (самополяризуемость) и p12 для p-системы пентадиенильного радикала.
Решение: Учитывая, что в радикалах есть орбитали, занятые одним электроном, общее выражение для поляризуемости имеет вид
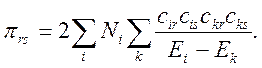
Используя вид молекулярных орбиталей для пентадиенильного радикала, представленный в методическом пособии по курсу «Строение вещества», можно определить табличные значения поляризуемостей (в единицах –(1/b))
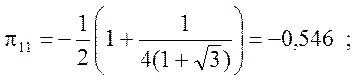
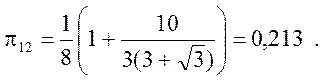
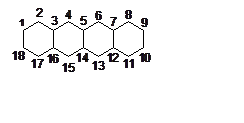 3. (400) По теории возмущений определить энергию и вид
нижней по энергии молекулярной орбитали тетрацена.
3. (400) По теории возмущений определить энергию и вид
нижней по энергии молекулярной орбитали тетрацена.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.