Определение количества молекулярных термов. Определение распределения спиновой плотности в радикале, страница 2

5. (300) Определить разрешен ли по четности дипольный переход между HOMO и LUMO орбиталями для циклической молекулы H_n (n = 4k+2, где k – целое число). HOMO – высшая занятая молекулярная орбиталь, LUMO – низшая свободная орбиталь.

Задачи на контрольную 28 декабря 2000, группы 841, 842, 743

1. (600) При радиолизе раствора перекиси водорода из-за ионизации молекул среды образуется плоский катион-радикал (Н₂О₂)⁺. Определить основной терм этой частицы. Строение катион-радикала представлено на рисунке.

2. (400) Найти распределение спиновой плотности для радикала Н₉, строение которого показано на рисунке.

3. (200) Определить основной терм линейной молекулы H-Ce³⁺-H.

4. (300) Две одинаковые циклические p-системы с N центрами каждая обьединяются в одну общую p-систему с 2N центрами (N = 4k+2). Определить изменение полной p-электронной энергии при таком объединении.

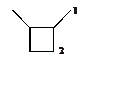
5. (500) Для p-системы, строение которой представлено на рисунке определить более предпочтительное направление радикального замещения по центрам 1 или 2 (неэквивалентность центров задается геометрией молекулы). Отметим, что в этой молекуле центры 1 не заместители, а группы CH₂ с p-центрами.

Контрольная 28 декабря 2001, группы (группы 941, 942, 943, 843)

1. (500) В циклическом p-радикале, состоящем из N = 4n + 1 центров, в два соседних центра вводится индуктивный заместитель (CH₃-группа, x = -0.1). Определить (количественно), как изменится спиновая плотность на этих центрах при присоединении заместителей. Привести ответ для N =1001.

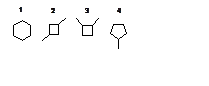
2. (300) Определить относительную стабильность геометрических изомеров с p-системами из 6 центров, показанных на рисунке.

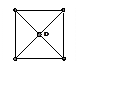
3. (400) Определить основной терм, количество и поляризацию переходов неспаренного электрона для комплекса TiH₆³⁺, имеющего строение плоского квадрата.

4. (300) Определить преимущественное направление радикального замещения для линейной молекулы с сопряженной p-системой из 6 центров (H₂C=CH-CH=CH-CH=CH₂). Нумеровать центры от края (1-2-3-4-5-6).

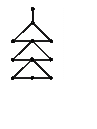
5. (500) Определить распределение спиновой плотности на Новогодней Елке H₁₁, строение которой показано на рисунке.

Задачи для контрольной 25 декабря 2002 года. Группы 041-043

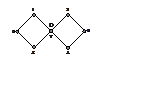
1. (600) Для радикала DH₆, строение которого показано на рисунке (плоская симметричная частица, группа симметрии D_2h), определить число линий поглощения, соответствующих разрешенным переходам, поляризацию и энергию этих линий, а также распределение спиновой плотности. Резонансные интегралы β_HH и β_HD считать одинаковыми.

2. (300) Определить табличные значения поляризуемости для p-системы аллильного радикала.

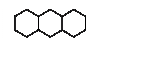
3. (400) По теории возмущений определить энергию и вид нижней по энергии молекулярной орбитали антрацена.

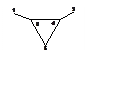
4. (400) Близится новый год – год черной козы и декабрь – время козерогов. Определите распределение спиновой плотности в p-системе из 5 p-центров, которая чем-то похожа на голову козы (см. рисунок).

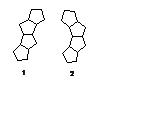
5. (300) Определить относительную стабильность p-систем изомеров, которые представлены на рисунке.

Задачи  на контрольной 29 декабря 2003 года. Группы 141-143

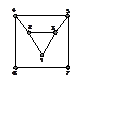
1. (500) Для радикала DH₄, строение которого показано на рисунке (плоская симметричная частица), определить число линий поглощения, соответствующих разрешенным переходам, поляризацию и энергию этих линий, а также распределение спиновой плотности. Резонансные интегралы β_HH и β_HD считать одинаковыми.

2. (300) Определить табличные значения поляризуемости p₁₁ (самополяризуемость) и p₁₂ для p-системы пентадиенильного радикала.

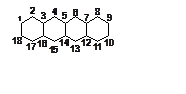
3. (500) По теории возмущений определить энергию и вид нижней по энергии молекулярной орбитали тетрацена.