Переход к комплексным числам ?
Можно 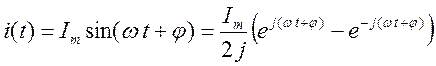
Но удобнее ввести комплексный ток вида ![]() - так, что реальный ток
- так, что реальный ток
![]()
- здесь ![]() - комплексная
амплитуда (содержит и амплитуду, и фазу)
- комплексная
амплитуда (содержит и амплитуду, и фазу)
![]() - аналогично комплексная
амплитуда напряжения
- аналогично комплексная
амплитуда напряжения
Говорят, что комплексные амплитуды ![]() символизируют
символизируют
![]()
------------------------------------------------------------------------------------------------------
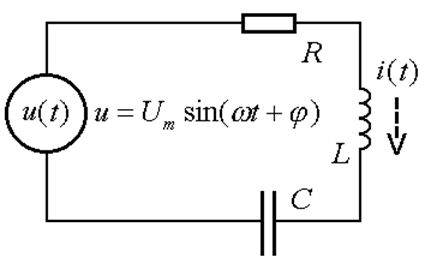
![]()
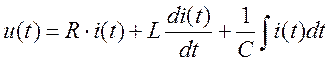 - где
- где ![]()
Введем
![]() ,
, ![]()
![]() ,
, ![]()
Подставляя в уравнение :
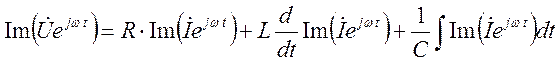
Операция взятия мнимой части коммутативна с вещественными операторами Þ
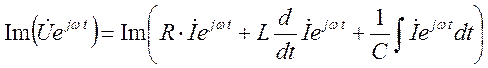
-
но под операторами ![]() - комплексные экспоненты,
соответствующие в комплексной плоскости векторам, вращающимся с частотой
- комплексные экспоненты,
соответствующие в комплексной плоскости векторам, вращающимся с частотой ![]() :
:
И
т.к. уравнение справедливо при любом ![]() , то равны не только
мнимые части, но и сами вектора. Т.е. :
, то равны не только
мнимые части, но и сами вектора. Т.е. :
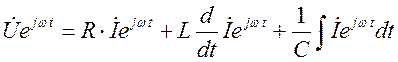 , или
, или
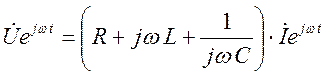 -
т.е.
-
т.е.
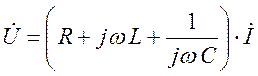
- закон Ома в комплексной
форме - ![]() , где
, где
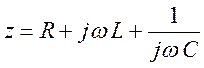 - комплексное сопротивление ;
- комплексное сопротивление ;
вообще ![]() , где
, где
![]() - активная составляющая сопротивления ,
- активная составляющая сопротивления ,
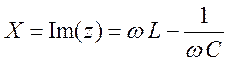 - реактивная составляющая
- реактивная составляющая
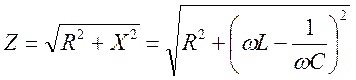 - модуль полного сопротивления
- модуль полного сопротивления
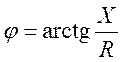 -
фазовый сдвиг
-
фазовый сдвиг
Комплексная амплитуда тока будет (по правилу деления комплексных чисел) :
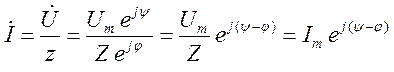
-
далее переходя к вещественной
форме (домножая на ![]() и беря
и беря ![]() )
:
)
:
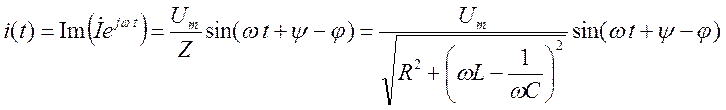 ,
,
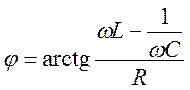 - причем эти соотношения можно получить
прямым решением интегро-дифференциального уравнения
- причем эти соотношения можно получить
прямым решением интегро-дифференциального уравнения
------------------------------------------------------------------------------------------------------
Аналогично вводится комплексная проводимость :

Обратно, 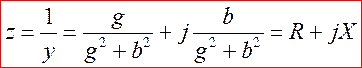
------------------------------------------------------------------------------------------------------
Ранее мы нормировали ![]() на
на ![]() - на
амплитудные значения;
- на
амплитудные значения;
но часто комплексные амплитуды нормируют на действующие
значения 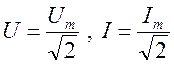 - т.е.
- т.е. ![]() ,
, ![]()
В этом случае можно ввести "комплексную" мощность
![]()
- где ![]() - разность фаз тока и
напряжения ; тогда :
- разность фаз тока и
напряжения ; тогда :
![]() - активная мощность в цепи
- активная мощность в цепи
![]() - реактивная мощность
- реактивная мощность
![]() - полная (кажущаяся) мощность
- полная (кажущаяся) мощность
------------------------------------------------------------------------------------------------------
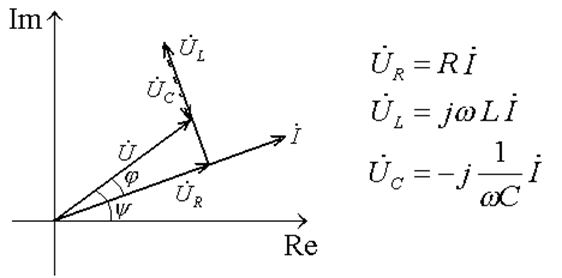
Для пояснения действия участков цепей и для расчета простейших схем применяют метод векторных диаграмм .
------------------------------------------------------------------------------------------------------
Обычно - применяют т.н. символический метод - заменяют в рассчитываемой линейной схеме индуктивности и емкости соответствующими комплексными сопротивлениями и далее рассчитывают схему, решая систему линейных алгебраических уравнений, которую составляют на основе законов Ома и Кирхгофа :
![]()
![]()
![]()
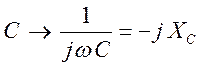
![]()
------------------------------------------------------------------------------------------------------
Пример : расчет пускового тока люминесцентной лампы :
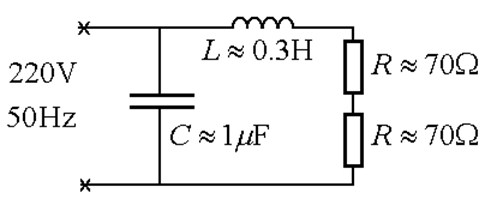
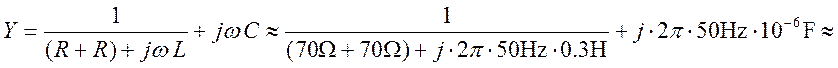
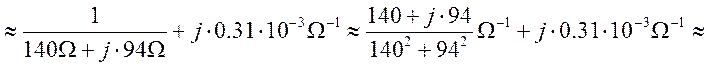
![]()
![]()
------------------------------------------------------------------------------------------------------
На самом деле : почему можно заменять вещественные синусоидальные токи и напряжения комплексными экспонентами ?
- т.к. система предполагается линейной, и при ее прохождении вещественные сигналы остаются вещественными, мнимые - мнимыми (т.к. все операторы, описывающее действие системы на сигналы, - вещественные) :
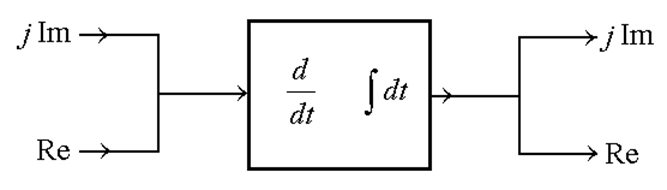
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.