Проинтегрируем кинетическое уравнение для простейшей обратимой реакции
А
![]() В.
В.
при начальных
условиях CA(0) = a, CB(0) = 0. Учтем, что
CA = a – CB.
Уравнение для изменения концентрации B имеет вид
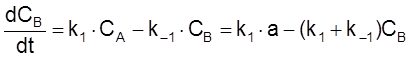 ,
,
ß
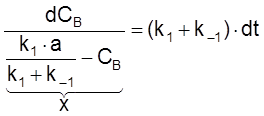 ,
,
ß dCB = –dx
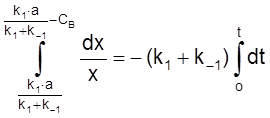 ,
,
ß
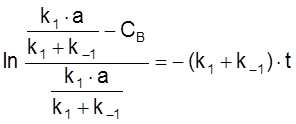 ,
,
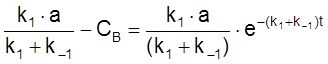 ,
,
ß
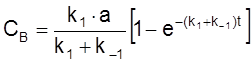 .
.
Найдем теперь CA, учитывая, что CA + CB = a:
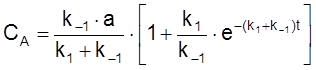 .
.
Введем константу равновесия
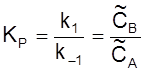
и время релаксации
t 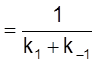 .
.
Тогда
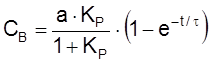 ,
,
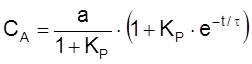 ,
,
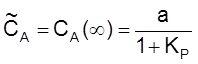 ,
, 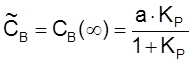 ,
,
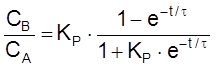 ,
,
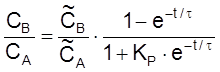 .
.
Видим, что характеристическое время установления равновесия
t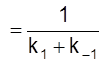
определяется суммой констант скоростей прямой и обратной реакции.
График зависимости CA и CB от t (для KP > 1) изображен на рис. 2.6.
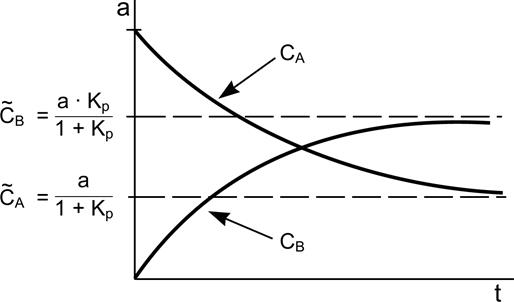
Рис. 2.6. Кинетические кривые для обратимой реакции А ![]() В
В
Если k1 >> k–1 (т. е. KP >> 1 и равновесие сдвинуто вправо), то
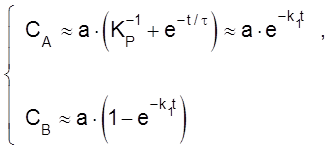
до достаточно больших t >> t.
Как видим, в этом случае кинетика описывается теми же уравнениями, что и для необратимой реакции A ® B, т. е. обратную реакцию можно не учитывать.
Аналогичным способом можно рассмотреть обратимые реакции и более высокого порядка.
Если открытая система поддерживается в термодинамически неравновесных условиях, в ней могут устанавливаться так называемые стационарные состояния, когда концентрации не изменяются во времени, поскольку скорость подвода частиц в систему или их отвода из системы равна скорости их расхода или образования в реакции.
Пусть скорость подвода частиц равна Wo. Для определенности примем Wo > 0, хотя в общем случае Wo = W+ – W– (где W+ и W– – скорости подачи и отбора частиц, соответственно) может быть как больше, так и меньше нуля.
Пусть далее частицы расходуются в реакции. Скорость реакции в соответствии с законом действующих масс есть степенной многочлен L(C).
Тогда кинетическое уравнение
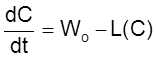 ,
(2.16)
,
(2.16)
причем в системах с
единственным стационарным состоянием L(C) – монотонно возрастающая функция
концентрации. Следовательно, ![]() есть монотонно
убывающая функция концентрации.
есть монотонно
убывающая функция концентрации.
Из уравнения (2.16) следует, что
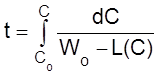 .
.
Рассмотрим состояние системы при t ® ¥. Здесь в принципе возможны два состояния:
1) C ® ¥;
2) Wo – L(C) ® 0.
Другими словами, в открытых системах рассматриваемого типа концентрация либо неограниченно возрастает, либо стремится к постоянному стационарному значению, которое соответствует уравнению
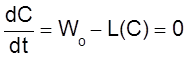 .
.
При этом уравнение ![]() имеет
только один корень, так как функция L(C) – монотонно возрастающая, и,
следовательно,
имеет
только один корень, так как функция L(C) – монотонно возрастающая, и,
следовательно, ![]() может иметь только один нуль.
может иметь только один нуль.
Рассмотрим сначала случай, когда ![]() ,
т. е. реакция вообще отсутствует. Тогда
,
т. е. реакция вообще отсутствует. Тогда
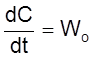
и
![]() .
.
«Включение» реакции уменьшает скорость тем больше, чем больше концентрация. Поэтому качественно для изменения концентрации будет наблюдаться картина, изображенная на рис. 2.7.
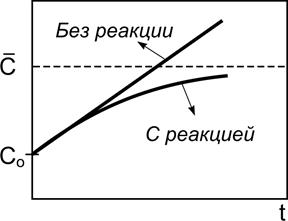
Рис. 2.7. Кинетические кривые
для накопления частиц в открытой системе при Wo > 0 в отсутствие
и в присутствии химической реакции, приводящей к гибели частиц
Нижняя кривая соответствует установлению стационарной
концентрации ![]() , определяемой из условия
, определяемой из условия
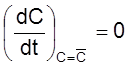 .
.
За какое время будет устанавливаться стационарное состояние? Чтобы ответить на этот вопрос, заметим, что постоянные времени, которые входят в уравнение (2.16), должны быть такими же, как и для однородного уравнения
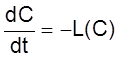 ,
,
описывающего поведение замкнутой системы.
Рассмотрим это на двух конкретных примерах.
а) Накопление частиц с данным (постоянным) временем жизни t при постоянной скорости генерации Wo
Пример – генерация возбужденных частиц светом и их спонтанная деактивация.
Имеем процесса типа A ® X. Кинетическое уравнение имеет вид
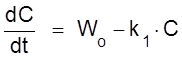 ,
, 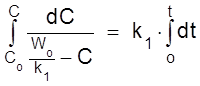 .
.
Его решение при Co = 0
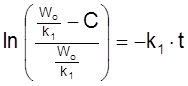 ,
,
Я
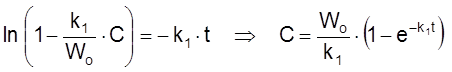 .
.
Видим, что:
1) время релаксации действительно равно времени релаксации t ![]() для закрытой системы;
для закрытой системы;
2) при t
>> ![]() устанавливается стационарная концентрация
устанавливается стационарная концентрация
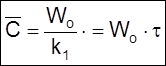 ,
(2.17)
,
(2.17)
соответствующая условию
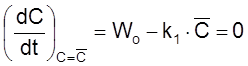 .
.
б) Накопление частиц, гибнущих в бимолекулярной реакции 2A ® X
Пример – генерация светом свободных радикалов и их гибель путем рекомбинации. В этом случае кинетическое уравнение имеет вид
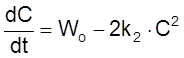 ,
,
причем 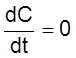 при
при
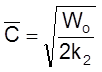 .
.
Проинтегрируем кинетическое уравнение при Co = 0:
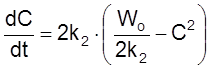 ,
,
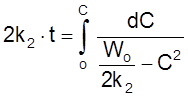 ,
,
ß
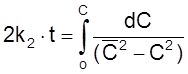 .
.
Интеграл в правой части этого уравнения – табличный:
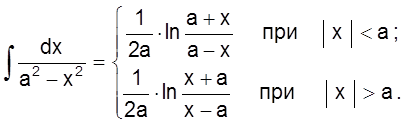
С учетом этого наше кинетическое уравнение принимает вид
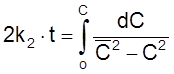 ,
,
ß
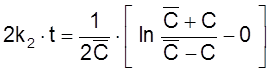 ,
,
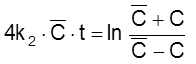 ,
,
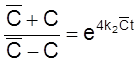 ,
, ![]() ,
,
![]() ,
,
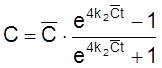 ,
,
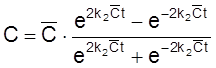 .
.
Отметим, что
t 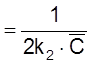
равняется (как было показано в разд.
2.1.3) характеристическому времени для бимолекулярной реакции в замкнутой системе
при ![]() .
.
Полезно убедиться, что в этом случае, как и в случае «а», выполняется условие (2.17): C = Wot .
Действительно, из
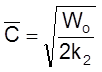 ,
,
т. е.
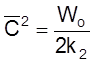 и t
и t 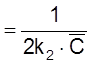
или
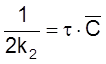 ,
,
имеем
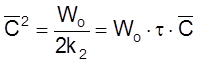 ,
,
ß
![]() .
.
Соотношение типа (2.17) весьма полезно для оценки стационарной концентрации в различных ситуациях.
Кинетические уравнения представляют собой один из видов уравнения материального баланса.
До сих пор мы рассматривали только изотропные системы, т. е. считали концентрации одинаковыми во всех точках системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.