Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (курсовая работа), страница 6

Найдем полюсы данной функции:

.

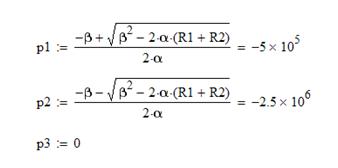
Оригинал будем искать с помощью теории вычетов:

.

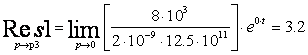
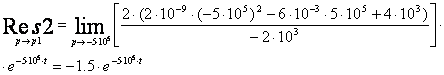
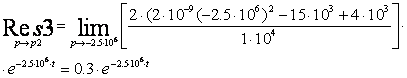
Тогда функция перехоного процесса:

, где

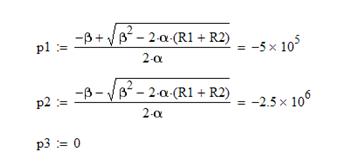
График переходного процесса:

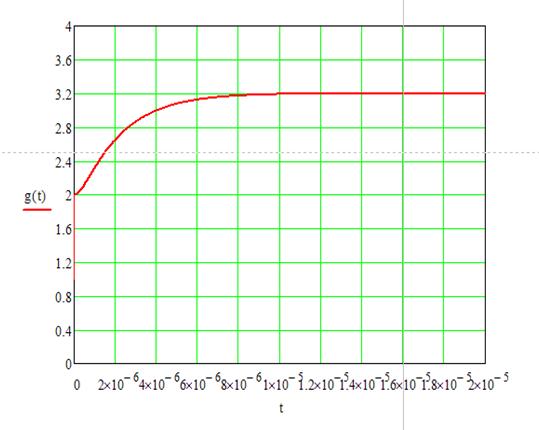
Рисунок 15.  Переходная характеристика цепи.

5.2. Определение импульсной характеристики цепи.

Импульсной характеристикой цепи h(t) является реакция цепи на воздействие входного сигнала, который описывается δ-функцией.

Так как , то можно записать:

.

График импульсной характеристики:

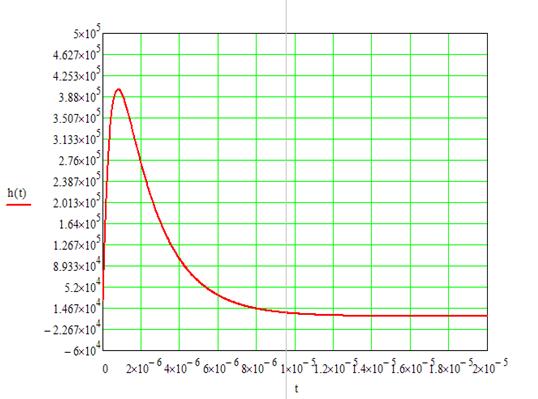
Рисунок 16.  Импульсная характеристика цепи.

6. Спектральный анализ выходного сигнала.

6.1. Определение спектральной плотности выходного сигнала.

Спектральная плотность выходного сигнала определяется выражением:

Подставив формулы, получим:

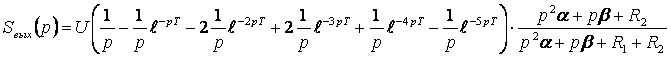
Определим выражение  спектральной плотности выходного сигнала, заменив оператор р на jω и воспользовавшись предыдущими расчетами:

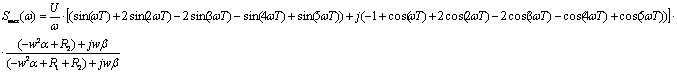 Подставим численные значения:

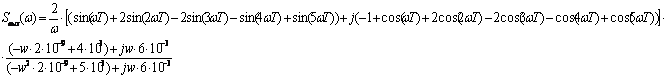6.2. Амплитудный спектр выходного сигнала.

Амплитудный спектр выходного сигнала есть модуль спектральной плотности. Согласно этому можно записать:

Подставив численные значения, получим формулу:

 График амплитудного спектра выходного сигнала:

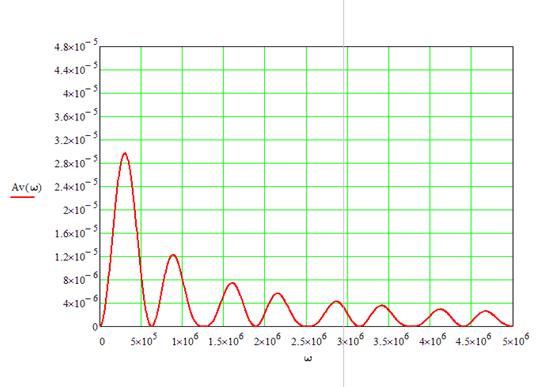
Рисунок 17. Амплитудный спектр выходного сигнала.

6.3. Фазовый спектр выходного сигнала.

Фазовый спектр выходного сигнала равен аргументу спектральной плотности выходного сигнала. Формула имеет вид:

График фазового спектра выходного сигнала:

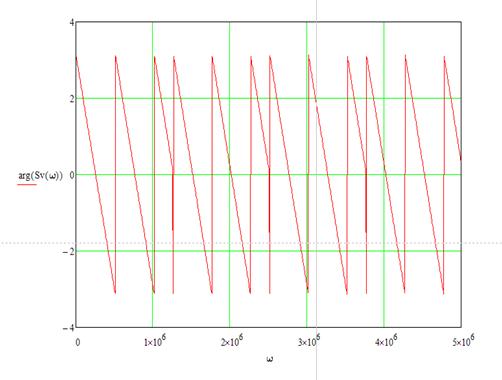
Рисунок 18. Фазовый спектр выходного сигнала.

7. Выходной сигнал.

Спектральная плотность выходного сигнала определяется выражением: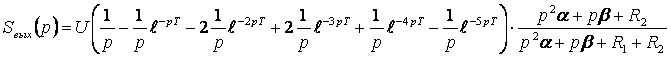

     Введем обозначение:

,

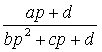тогда:

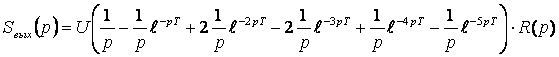
По расчетам, проведенным в предыдущих пунктах работы, запишем оригинал R(р):

С учётом этого запишем выходной сигнал:  

     График выходного сигнала приведён на рисунке 19:

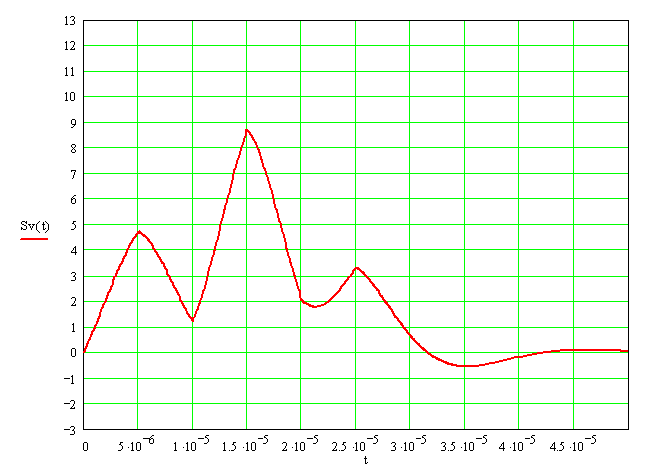
Рисунок 19. Выходной сигнал.

Анализ сигнала в EWB

Схема для построения переходной характеристики: