Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (курсовая работа), страница 2

Задание на курсовую работу

Тема работы: Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами.

ВАРИАНТ ЗАДАНИЯ

1. Схема электрическая принципиальная:       4

2. Входной сигнал: 2

3. Параметры элементов цепи и сигнала: 7

РАССЧИТЫВАЕМЫЕ ХАРАКТЕРИСТИКИ

1.  Спектральная плотность входного сигнала, амплитудный и фазовый спектр, ширина спектра.

2.  Частотный коэффициент передачи цепи, АЧХ, ФЧХ.

3.  Импульсная и переходная характеристики цепи.

4.  Спектральная плотность выходного сигнала, амплитудный и фазовый спектр, ширина спектра.

5.  Выходной сигнал.

СОДЕРЖАНИЕ ЗАПИСКИ

В записке привести подробный корреляционный и спектральный анализ заданного сигнала и прохождения его через заданную цепь. Определить интервал корреляции, ширину спектра входного и выходного сигналов. Математические выкладки должны быть обоснованы и прокомментированы. Материал следует иллюстрировать рисунками: обязательно построение графиков входного и выходного сигналов; их амплитудных и фазовых спектров; корреляционной функции входного сигнала; схемы цепи; амплитудно-частотной, фазочастотной, импульсной и переходной характеристик цепи.

Записка должна быть оформлена в соответствии с СТП 1.101-2002.

1.  Исходные данные.

1.1. Схема электрическая принципиальная:

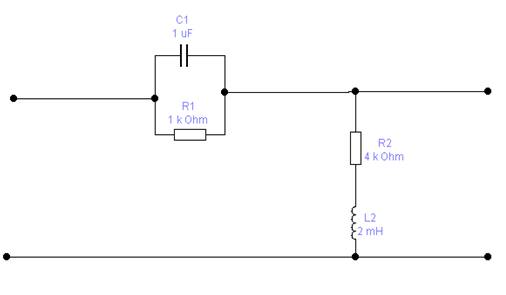
Рисунок 1.  Схема электрическая принципиальная.

1.2. Входной сигнал имеет вид:

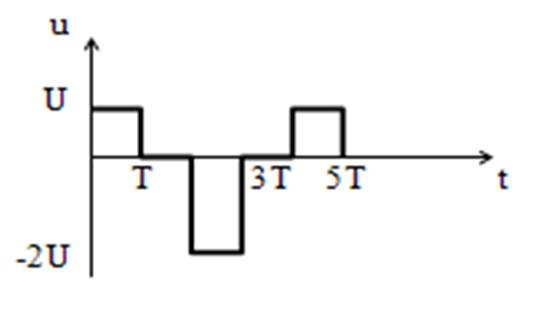
Рисунок 2. Исходный входной сигнал.

1.3. Параметры элементов цепи и сигнала:

Таблица 1 -  Параметры элементов цепи и сигнала

C1, нФ	С2, нФ	L1, мГн	L2, мГн	R1, кОм	R2, кОм	U, В	T, мкс
1	2	2	2	1	4	2	5

2.  Корреляционная функция входного сигнала.

Важнейшей временной характеристикой является автокорреляционная функция (АКФ), позволяющая судить о степени связи (корреляции) сигнала и его смещенной во времени копии. АКФ равна скалярному произведению сигнала и копии:

Математическая модель входного сигнала имеет вид:

Графически входной сигнал имеет вид:

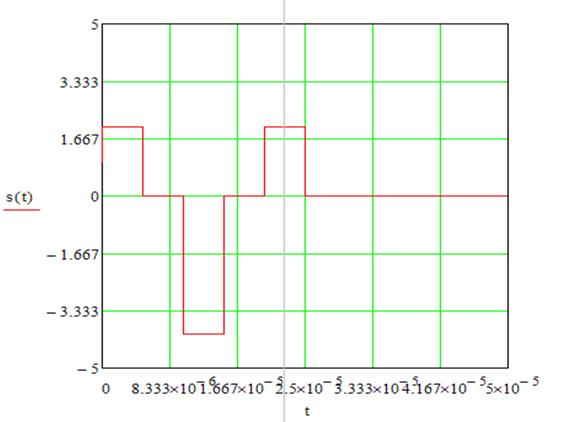
Рисунок 3. Входной сигнал, построенный в Mathcad.

 Зная, что корреляционная функция четна, рассмотрим ее на интервале              . Где τ-интервал смещения сигнала во времени.

Корреляционная функция на интервале (0;5Т) определяется суммой корреляционных функций на каждом из интервалов.